Ich wollte mich schon immer mal mit Funkkram beschäftigen! Und so hatte ich mir auf Iiie-Bäh so einen billigen RTL-Tuner bestellt – quasi Funkscanner für Arme. Immerhin ist es die Edelvariante des Proletariatsscanners, denn meiner hat vom netten Chinesen ein hübsch blaues Alugehäuse und eine externe Antenne spendiert bekommen:

lsusb erkennt ihn prompt:

Bus 001 Device 060: ID 0bda:2838 Realtek Semiconductor Corp. RTL2838 DVB-T

Schönes Spielzeug dachte ich mir.

Worum es heute geht, ist irgendwas sinnvolles damit zu tun, damit meine Frau nicht behaupten kann, ich würde immer nur Kram bestellen, aber nix sinnvolles damit machen. Ich fürchte zwar, dass unsere Definitionen von sinnvoll divergieren, aber einen Versuch ist es wert.

Also frisch ans Werk! Das erste Funkobjekt, das mir ins Auge fiel war unsere chinesische Wetterstation. Die kann Signale von Funksensoren für Temperatur und Luftfeuchtigkeit empfangen. Laut Hersteller funken die Sensoren auf 433.92 MHz. Wäre doch schön, so einen Sensor mal zu belauschen. Wenn das gut funktioniert, wäre es reizvoll, noch mehrere davon anzuschaffen und zum Big-Brother der Zimmertemperatur zu werden. Und so sieht mein Sensor-Exemplar aus:

Großer Lauschangriff

Als erstes wollen wir mal versuchen, ob wir da überhaupt sowas wie ein Signal zu sehen bekommen. Nur wie? Die Suchmaschine meines Vertrauens sagte mir, dass es da ein Tool namens gqrx gibt, das mit solchen SDRs (software defined radios) reden kann und zur Exploration geeignet sei. Also her damit:

sudo apt-get install gqrx-sdr

Und gleich starten:

gqrx

Die richtige Hardware auswählen und schon gibt's was zu sehen und zu hören. Konkret bekommt man ein schönes Frequenzspektrum um die Gegend die man ausgewählt hat, sowie ein Wasserfalldiagramm und ein demoduliertes Audiosignal. Das hat was von der Jagd nach Außerirdischen! Wobei – ein sehr irdischer Sensor wäre ja auch schon ein Erfolg.

Nach ein bisschen Rumspielen hatte ich den Dreh mit der Software grob raus und habe mal die fragliche Frequenz eingestellt und abgewartet. Und siehe da – es tut sich was. Nicht direkt auf der Zielfrequenz, aber ganz in der Nähe:

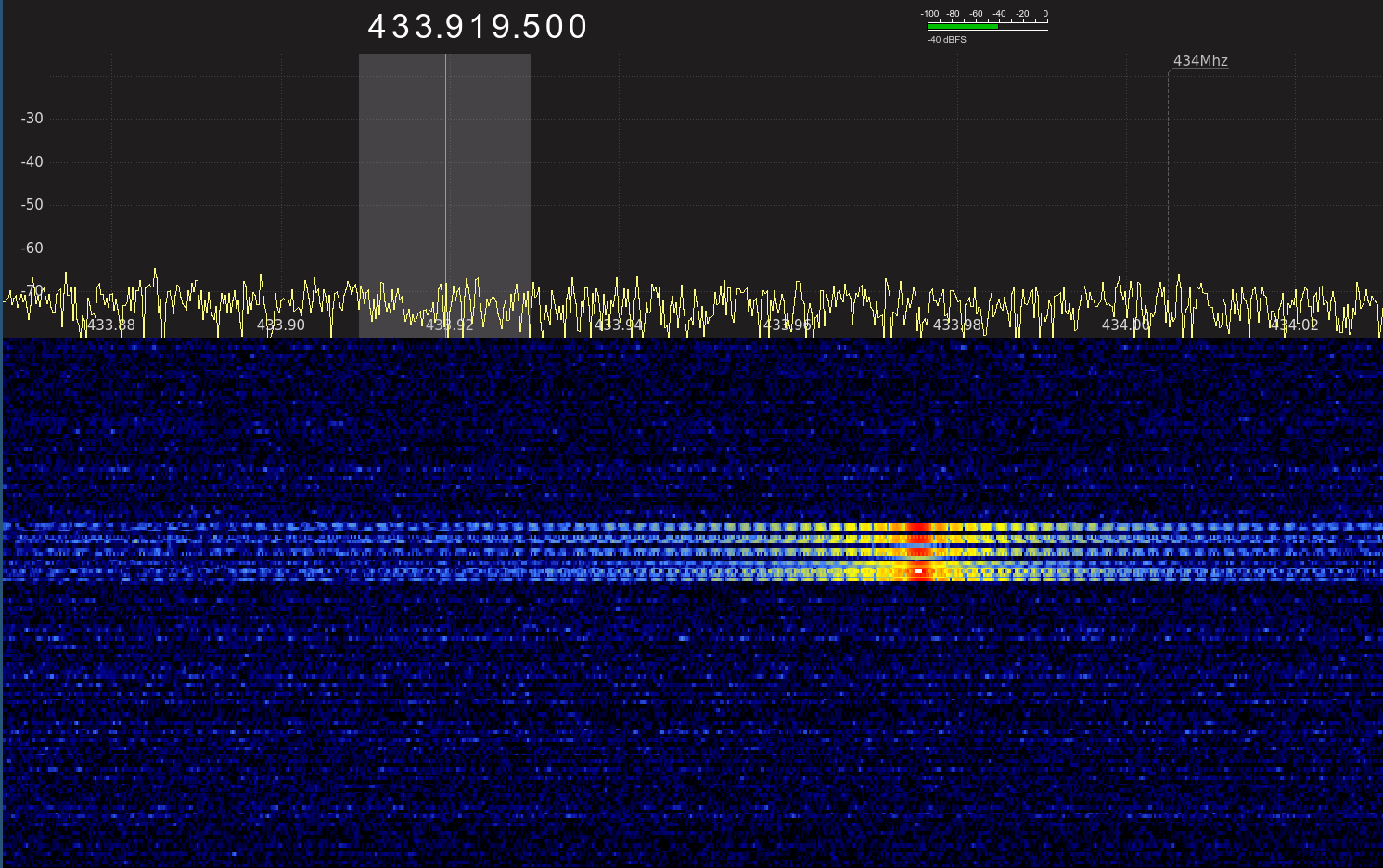
Also nix wie da hin, d.h. Frequenz entsprechend nachstellen und wieder warten. Eine gute Minute später wurde ich mit einem neuen Signal belohnt – und diesmal habe ich es genau erwischt mit meinem Screenshot:

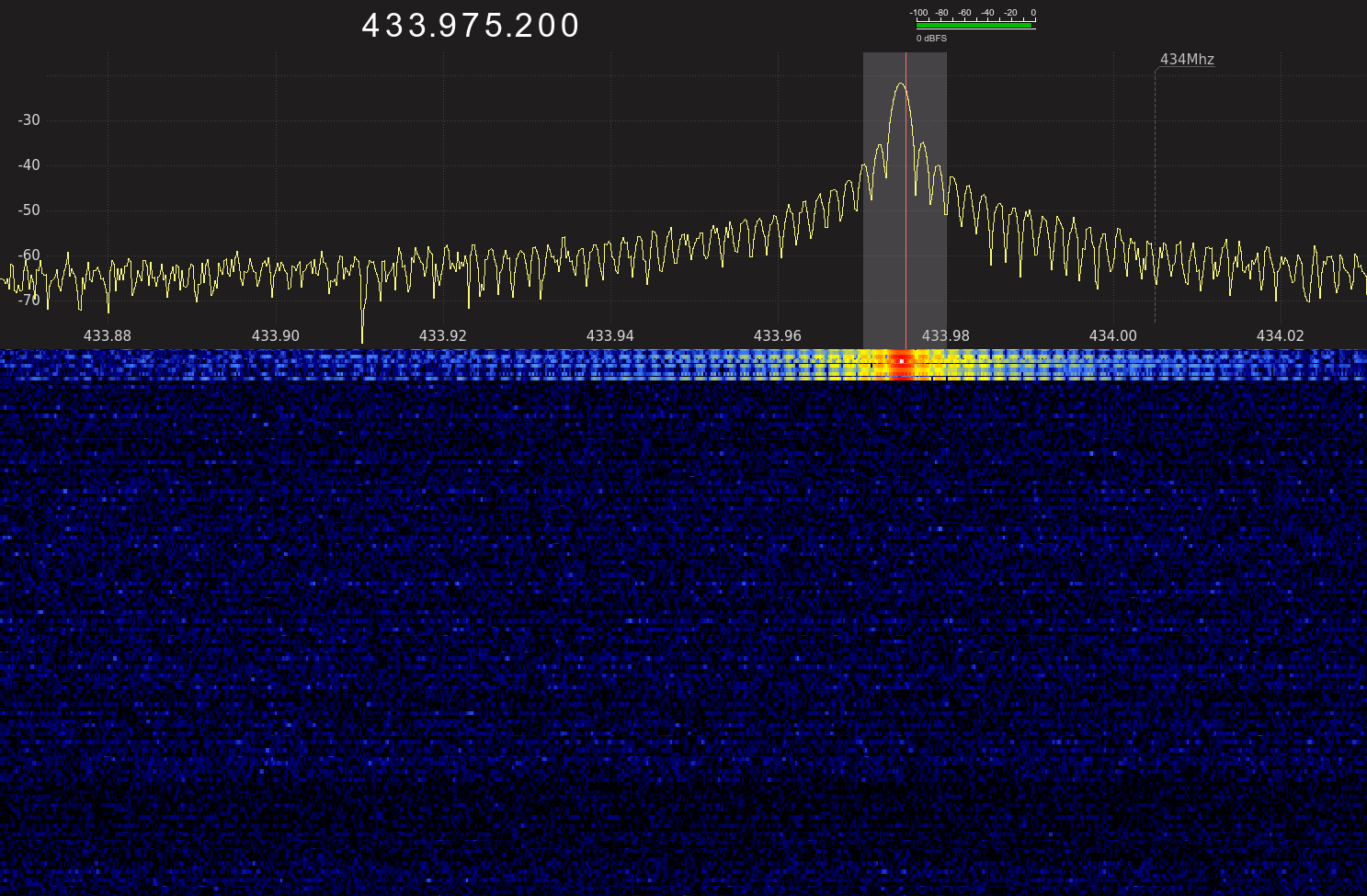
Diesmal passt die Frequenz fast perfekt. Und auf dem Ohr (mit Amplituden-Demodulation) klingt das dann so:

Sehr cool! Das ist doch schonmal ein erster Erfolg. Aber wie komme ich an den Inhalt dieses Signals. Und ist das auch wirklich mein Sensor, oder evtl. Nachbar's Garagentoröffner? Letzteres scheidet aber eigentlich aus, denn das Signal kommt regelmäßig alle 70 Sekunden oder so. Und es wird auch schwächer, wenn ich den Sensor in einen weiter entfernten Raum stelle.

Zunächst habe ich mir das Audio-Signal mal in Audacity genauer angesehen:

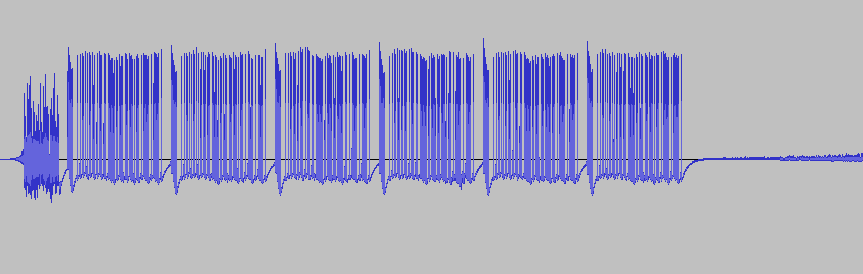
Hübsch. Schaut für mich aus, wie sechs distinkte Signalgruppen. Nun bin ich sicher nicht der erste, der sowas dekodieren will und so habe ich mich wieder auf die Suche gemacht und bin auf rtl_433 gestoßen. Das ist ein Stück Software, das gängige Signale mit rtl-sdr und anderer Hardware empfangen und dekodieren kann. Das brauch' ich!

# Repository clonen
git clone https://github.com/merbanan/rtl_433/
# Dependencies installieren
sudo apt-get install libtool libusb-1.0-0-dev librtlsdr-dev rtl-sdr build-essential autoconf cmake pkg-config
# Kompilieren
mkdir build
cd build
cmake ..
make
# Und installieren
sudo make install

Das muss natürlich sofort ausprobiert werden. Also starten und abwarten:

❯ rtl_433
rtl_433 version 20.11 branch master at 202011122224 inputs file rtl_tcp RTL-SDR
Use -h for usage help and see https://triq.org/ for documentation.
Trying conf file at "rtl_433.conf"...
Trying conf file at "/home/users/pagel/.config/rtl_433/rtl_433.conf"...
Trying conf file at "/usr/local/etc/rtl_433/rtl_433.conf"...
Trying conf file at "/etc/rtl_433/rtl_433.conf"...
Registered 145 out of 175 device decoding protocols [ 1-4 8 11-12 15-17 19-21 23 25-26 29-36 38-60 63 67-71 73-100 102-105 108-116 119 121 124-128 130-149 151-161 163-168 170-175 ]
Found Rafael Micro R820T tuner
Exact sample rate is: 250000.000414 Hz
[R82XX] PLL not locked!
Sample rate set to 250000 S/s.
Tuner gain set to Auto.
Tuned to 433.920MHz.
Allocating 15 zero-copy buffers

Und nach einer Weile kam dies:

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 
time      : 2020-11-15 18:41:54
model     : inFactory-TH ID        : 135
Channel   : 1            Battery OK: 1             Temperature: 68.00 F      Humidity  : 59 %          Integrity : CRC
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 
time      : 2020-11-15 18:41:55
model     : inFactory-TH ID        : 135
Channel   : 1            Battery OK: 1             Temperature: 68.00 F      Humidity  : 59 %          Integrity : CRC
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 
[..]

Seeeehr gut! Also außer, dass so bescheuerte Einheiten wie Fahrenheit eigentlich unter meiner Würde sind. Aber das ist leicht zu reparieren:

❯ rtl_433 -C si
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
time      : 2020-11-15 21:01:03
model     : inFactory-TH ID        : 135
Channel   : 1            Battery OK: 1             Temperature: 20.17 C      Humidity  : 59 %          Integrity : CRC
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

Perfekt! Diese Message kommt übrigens immer sechs mal, bevor dann wieder ≈70 Sekunden Ruhe war und neue sechs Messages kamen. Die genaue Frequenz scheint nicht sooo wichtig zu sein, denn es hat ja geklappt, obwohl die nicht ganz stimmte. Ich habe es dann natürlich auch nochmal mit der richtigen Frequenz probiert:

rtl_433 -f 433975000
[...]
Sample rate set to 250000 S/s.
Tuner gain set to Auto.
Tuned to 433.975MHz.
[...]

Hat genauso funktioniert. Aber was für ein Protokoll verwendet das Ding? Auch das, und einiges mehr, kann man herausfinden:

rtl_433 -C si -M protocol -M level
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 
time      : 2020-11-15 21:13:42                    Protocol  : 91
model     : inFactory-TH ID        : 135
Channel   : 1            Battery OK: 1             Temperature: 20.17 C      Humidity  : 59 %          Integrity : CRC
Modulation: ASK          Freq      : 434.0 MHz
RSSI      : -0.1 dB      SNR       : 25.5 dB       Noise     : -25.6 dB

Ah – also nun wissen wir, dass Protokoll 91 (inFactory, FreeTec NC-3982-913 temperature humidity sensor) verwendet wird. Und auch die Fequenz hat er offenbar selber justiert (434.0MHz).

Unter Modulation steht da "ASK" – das steht für Amplitude Shift Keying und ist die gleiche Modulation, die das DCF77 Signal der Atomuhr in Deutschland verwendet. Im Wesentlichen ist das eine Art von digitaler Amplitudenmodulation, die hier ziemlich gut erklärt wird.

Spannend ist auch, dass neben den Messdaten auch Werte für Channel und ID geliefert werden, denn wenn man mehrere solche Sensoren im und um's Haus verteilen will, dann muss man ja auch irgendwie erkennen, welchen Sensor man genau vor sich hat. Für die Einstellung des Kanals gibt es im Batteriefach einen kleinen Schiebeschalter mit drei verschiedenen Positionen. Also liegt es nahe, dass die ID eine hart-codierte "Seriennummer" des jeweiligen Sensors ist. Allerdings einen recht kurze, denn irgendwie klingt "135" nicht nach einem riesigen Zahlenraum – wohl eher ein Byte. Da ist die Gefahr von ID-Kollisionen schon recht hoch.

Natürlich bin ich dieser Theorie empirisch auf den Grund gegangen und habe weitere 5 Sensoren gekauft, deren IDs auch alle im Zahlenraum unter 255 lagen. Und so habe ich im gewohnheitsmäßigen Selbstgespräch (Meine Frau interessiert sich nicht für solche Themen) die Beschränktheit des chinesischen Hardwareentwicklers verhöhnt und den traditionellen Nerd-Überlegenheitstanz absolviert. Also bis mir bei einem Sensor die Batterie beim rumspielen rausgefallen ist und er nach Wiedereinlegen der selbigen eine neue ID hatte. Was'n da los? Batterie raus und wieder rein: ID=192, nochmal: ID=125, nochmal: ID=92... OK – also nicht fix ans Gerät gekoppelt, sondern jedesmal zufällig gewählt, wenn die Batterie gewechselt wird. Nicht so gut, wie 128bit IDs, aber durchaus nicht unclever. Sorry – chinesischer Entwickler. Offenbar hast du dir was dabei gedacht. Aber lästig ist es trotzdem, dass man nach jedem Batteriewechsel den Sensor neu bei der Wetterstation oder dem Homeserver anmelden muss, weil die ID sich ändert. Aber das ist vermutlich zu verschmerzen.

Und wo ich das Batteriefach schon offen hatte, ist mir noch aufgefallen, dass da auch noch ein keiner TX-Knopf ist, der spontan das Aussenden eines Datenpakets auslöst. Das ist praktisch zum Analysieren, weil ich so nicht immer eine Minute warten muss, bis er wieder sendet.

Deep dive

Das war ja nun fast zu einfach, um Spaß zu machen! Also machen wir es uns mal ein bisschen schwerer und versuchen, das rohe Signal aufzuzeichnen und genauer unter die Lupe zu nehmen.

Dazu brauchen wir geeignetes Werkzeug – ein Weg ist z.B. rtl-sdr:

sudo apt-get install rtl-sdr

Und so können wir 1 Sekunde lang bei 434MHz und einer Sample-Rate von 1MS/s aufzeichen:

rtl_sdr -f 434e6 -s 1e6 -n 1e6 foo.dat

Allerdings müssen wir dann zur Auswertung ohnehin in R oder Python wechseln und so ist es vermutlich besser, gleich in Python zu starten. Dazu brauchen wir das pyrtlsdr Package:

python -m venv .venv
source .venv/bin/activate
pip install pyrtlsdr

Zum Analysieren nehmen wir numpy und Co – wo Ihr das herbekommt erkläre ich jetzt nicht extra.

Also auf geht's – als erstes nehmen wir mal ein Signal auf:

from rtlsdr import RtlSdr
import numpy as np
import pandas as pd
from matplotlib import pyplot as pl

# Configure radio
sdr = RtlSdr()
sdr.sample_rate = 1e6
sdr.center_freq = 434e6
sdr.gain = 5

# acquire ≈3 seconds worth of data
dat = sdr.read_samples(3*1024*1024)
sdr.close()

Sehr schön. Und wenn wir uns die aufgenommenen Daten mal anschauen finden wir dies:

>>> dat
array([-0.00392157-0.00392157j,  0.00392157-0.00392157j,
       -0.00392157+0.00392157j, ..., -0.00392157-0.00392157j,
       -0.00392157-0.00392157j,  0.00392157-0.00392157j])

Ein Array von komplexen Zahlen! Hm – warum das? Scheinbar muss man doch ein bisschen was von Signalen und RF-Technik verstehen, um in SDR-Spielchen einzusteigen. Na gut – dann belese ich mich eben. Z.B. hier oder hier. Nun bin ich etwas klüger und komplexe Zahlen machen plötzlich Sinn: So wie ich es verstehe, wurden hier beim Senden zwei Signale digital gemischt, die 90° Phasenverschiebung gegeneinander haben und die heißen bei den Funk-Heinis I und Q, was für in-phase bzw. quadrature steht. Auf diese Weise können nicht nur zwei Signale gemeinsam übertragen werden, sondern auch auf elegante Weise verschiedene Modulationsarten realisiert werden. Wenn Ihr das verstehen wollt, lest die obigen Quellen und schaut ein paar YouTube Tutorials dazu, denn das wirklich korrekt zu erklären, übersteigt aktuell noch meine Kompetenz in dem Feld.

Aber ich glaube genug kapiert zu haben, um mich weiter mit unserem Funksensor zu befassen. Als erstes wollen wir mal ganz simpel das Signal plotten – nur wie? Wie Ihr Euch erinnert ist es komplex... Also im ersten Anlauf auf die rabiate Tour: nur den Realanteil:

pl.plot(dat.real)
pl.xlabel("µs")
pl.ylabel("Signal")
pl.show()

Das Ergebnis sieht so aus:

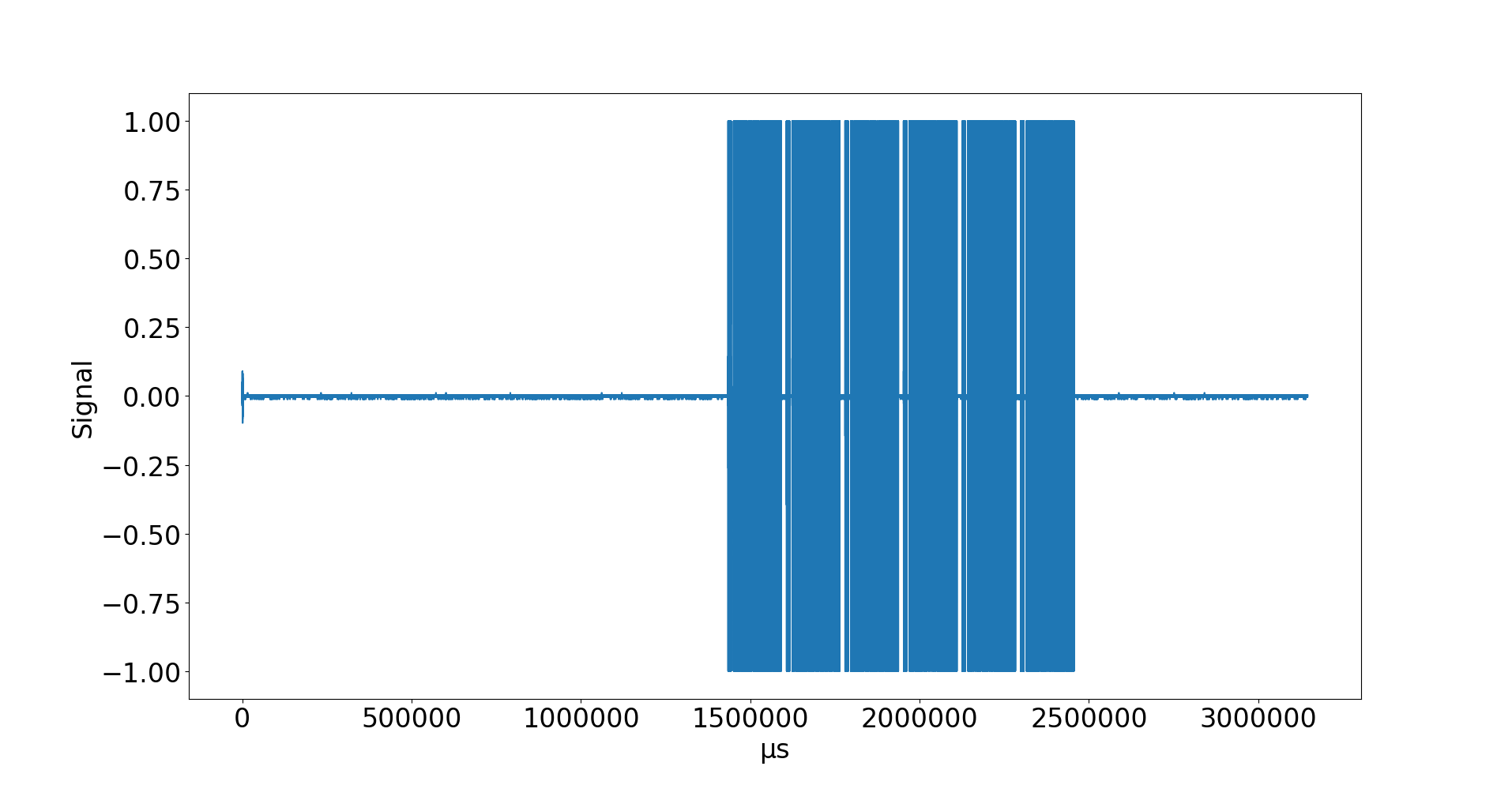
Also sechs Signalpakete, die auf die Entfernung identisch wirken. Mehr reinzoomen:

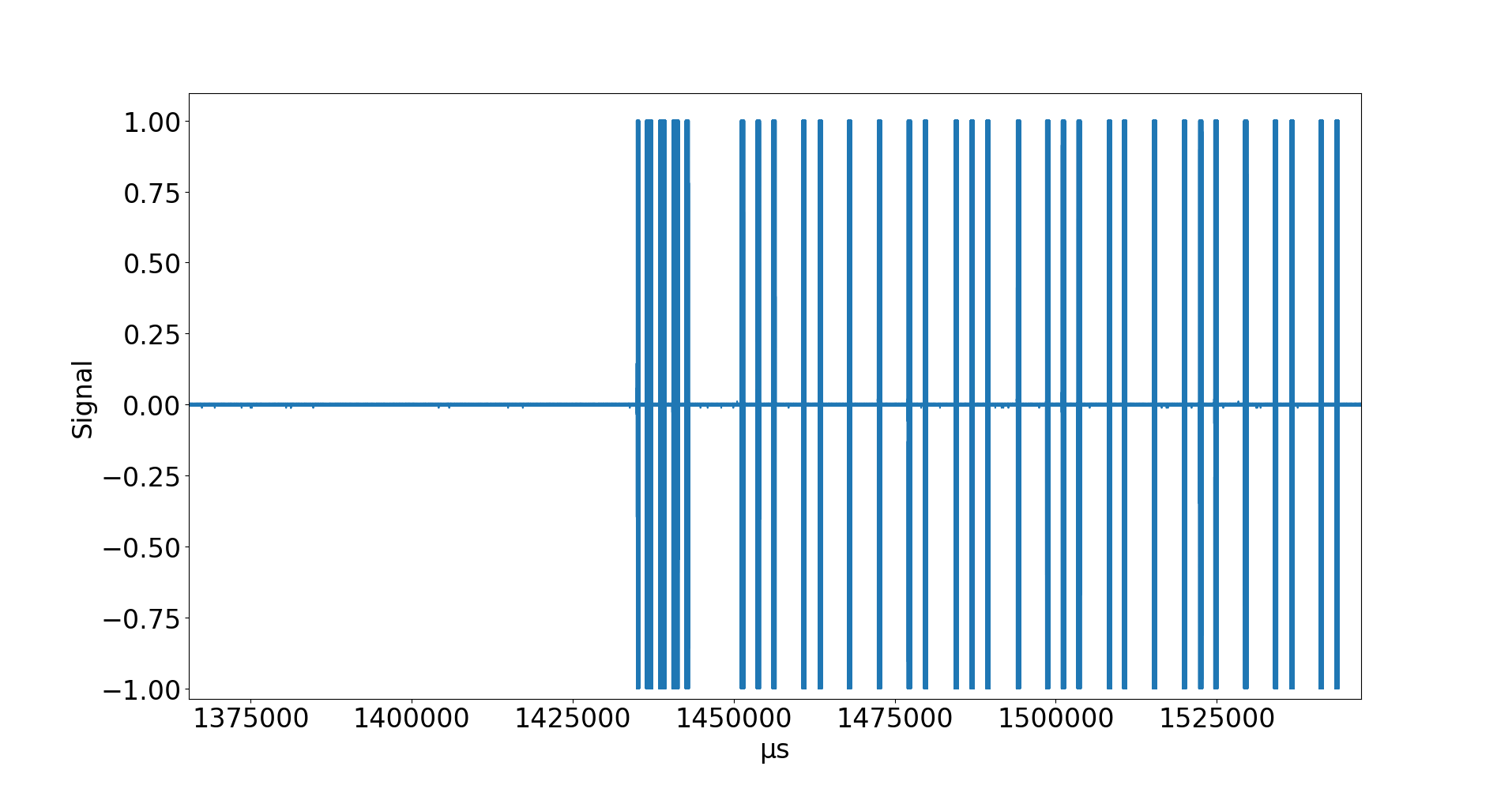
Und noch mehr:

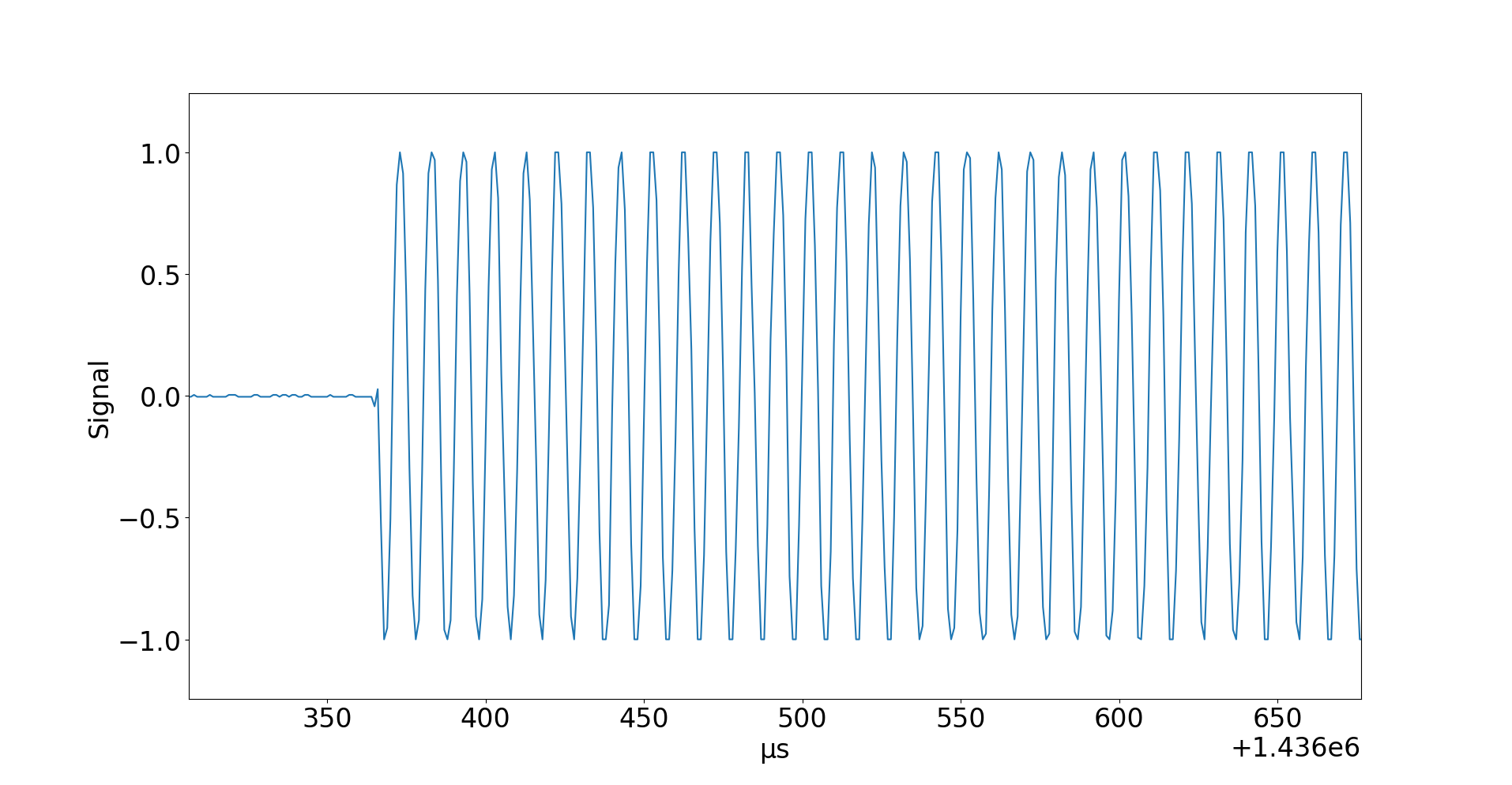
Ah – nun kann man das Baseband Signal schön erkennen. Mal ganz grob über den Daumen gepeilt sieht man 10 Perioden in einem Zeitraum von 100µs. D.h. die Baseband-Frequenz ist ungefähr

.

Das liegt klar über der Hörschwelle des Menschen, der Frequenzen im Bereich von ungefähr 20Hz – 20kHz wahrnehmen kann. Läge die Baseband-Frequenz z.B. bei 10kHz, dann hätte es am Anfang ganz schön im Ohr gepfiffen, als wir mit gqrx in das Spektrum hineingehört hatten. Gehört hatten wir aber schon etwas – und das liegt daran, dass dieses Baseband-Signal nicht konstant ist, sondern ja unsere Messwerte codieren muss. Und da die verwendete Signal-Codierung über eine Änderung der Amplitude läuft ist was zu hören. D.h. im Grunde werden hier kurze 100kHz Impulse gesendet, die von Stille, oder zumindest deutlich geringerer Leistung unterbrochen sind. Und wenn man weiß, wie lang ein Bit dauert, kann man das Signal decodieren.

Codeknacker

Bleibt die Frage, wie wir sowas decodieren können. Dazu wollen wir irgendwie die Baseband-Welle loswerden. Eine mögliche Methode, das quasi zu Fuß zu machen besteht darin, ein rolling mean zu berechnen – also den Mittelwert in einem Sliding/Rolling-Window. Im Endeffekt ist das ein simpler Tiefpassfilter.

Wir mussten vorhin schon verteufelt stark reinzoomen, um die Baseband-Frequenz sehen zu können. Insofern würde ich vermuten, dass es ok wäre, in einem Sliding-Window z.B. über 50µs zu mitteln. Weil unser Signal aber symmetrisch um Null oszilliert, sollten wir über den Absolutbetrag mitteln, statt über die Rohwerte.

Dann versuchen wir das mal – wieder nur für den Realteil:

dat = pd.DataFrame(np.abs(dat.real))
dat = dat.rolling(window=50).mean()

pl.plot(dat)
pl.xlabel("µs")
pl.ylabel("Signal")
pl.show()

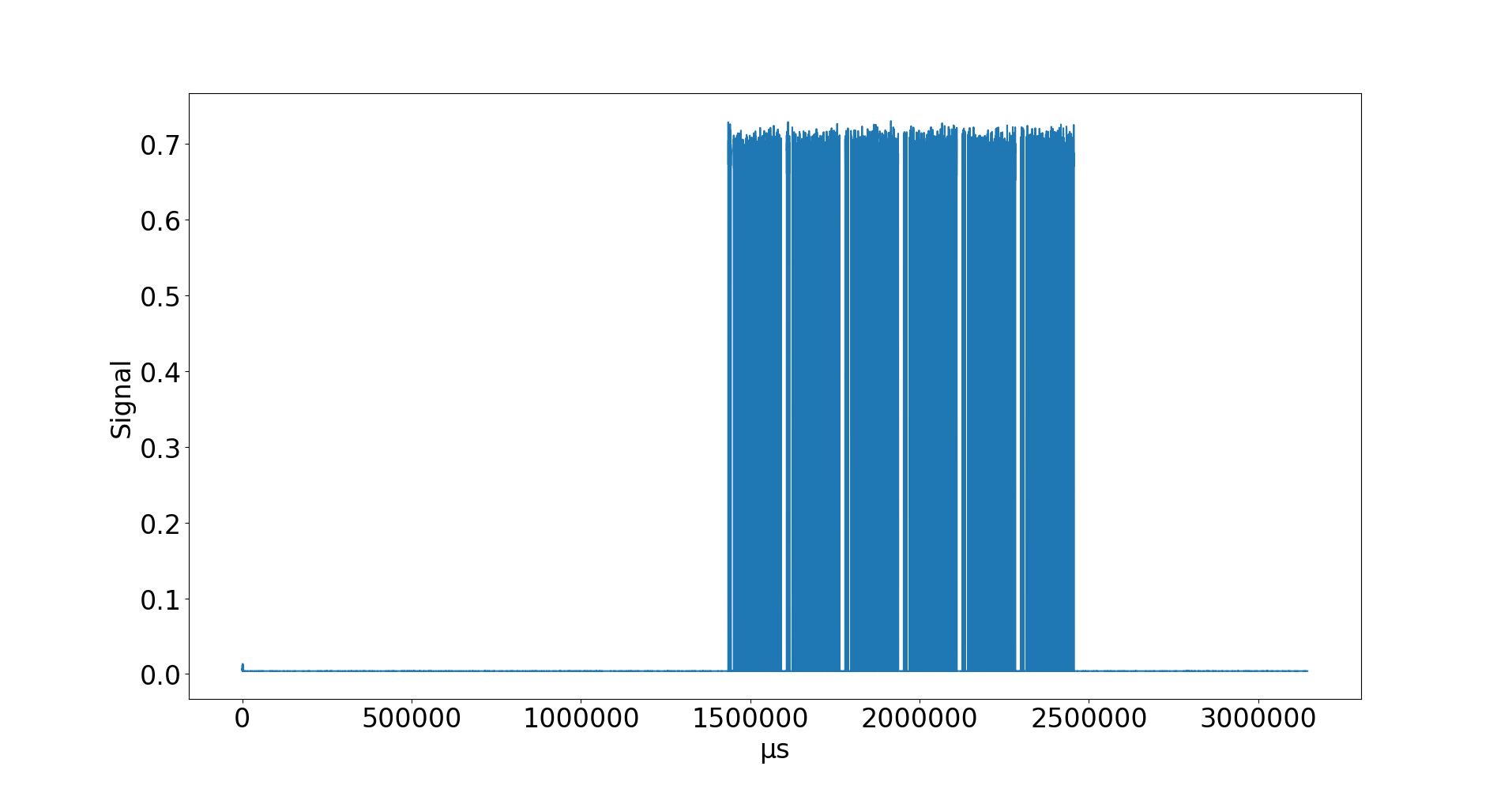
Ein bisschen reinzoomen:

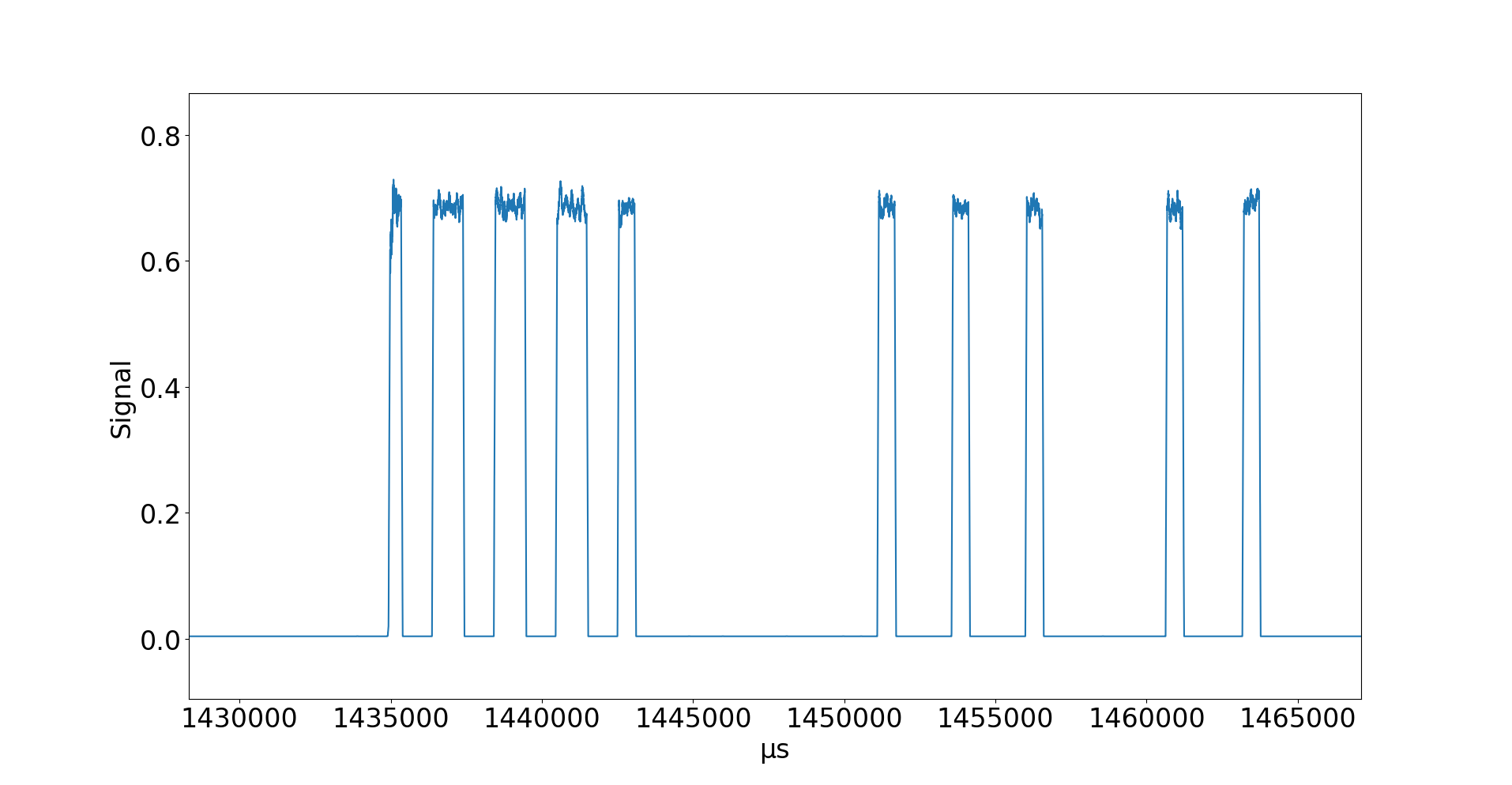
Das sieht doch schon ganz ordentlich aus! Man kann klar erkennen, dass es unterschiedlich breite Pulse gibt und vor allem unterschiedlich große Lücken zwischen den Pulsen.

Aber es geht noch cooler! Oben hatte ich die komplexen Zahlen und die beiden Signale in Quadrature erwähnt. Da wir zwei Teilsignale haben, die um 90° verschoben sind, stellt der Realanteil nur eine Projektion des eigentlichen Signals dar. Um nun an die Signalintensität zu kommen, müssen wir nur die maximale Amplitude berechnen und die ist gegeben durch:

wenn \(a\) und \(b\) der Real- bzw. Imaginäranteil von \(x\) sind. Also plotten wir das mal:

pl.plot(np.abs(dat))
pl.xlabel("µs")
pl.ylabel("Signal")
pl.show()

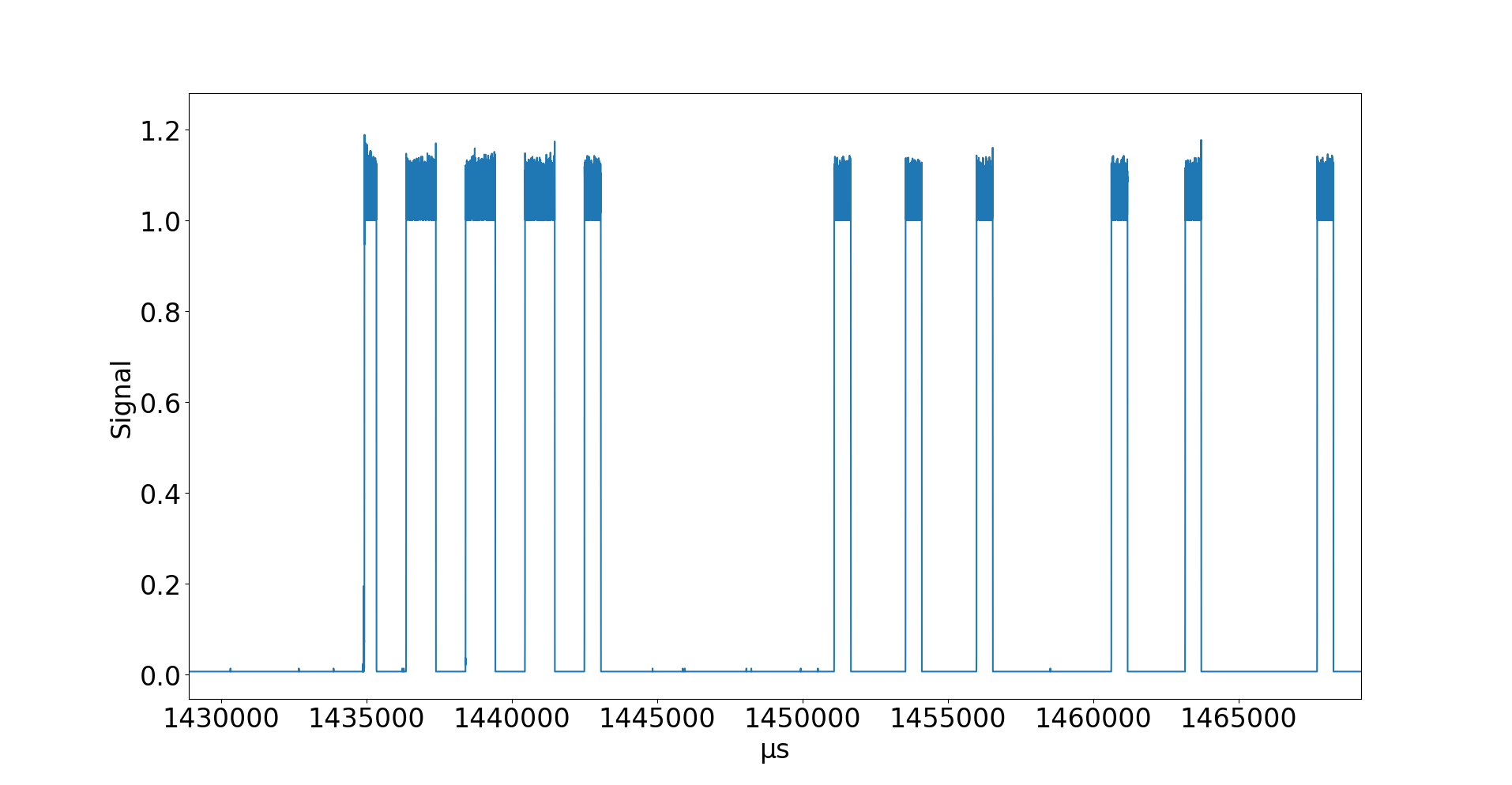
Ist das nicht toll? Wir haben die Pulse ganz ohne Filter extrahiert – einfach nur durch ein kleines Bisschen Arithmetik!

An dieser Stelle haben wir ein sehr schönes Signal. Wenn man jetzt noch einen Schwellenwert festlegt, dann bekommt man saubere Folgen von Nullen und Einsen. Als letztes fehlt dann noch die Länge des Intervalls, das ein Bit ausmacht, um eine schöne Bitfolge zu erhalten.

Und damit lasse ich es für heute bewenden. Wenn ich ganz viel Lust habe, versuche ich vielleicht noch, das komplett zu dekodieren. Aber für heute habe ich genug über SDR gelernt und bin erstmal zufrieden.