Wie kocht man ein Frühstücksei?

Posted on Mo 26 August 2019 in Science & Medicine

Das Frühstücksei – fester Bestandteil des deutschen Sonntagsfrühstücks und Quell von Freude, Lust und Frust. Letzteres v.a. wenn das Objekt der Begierde zu weich oder zu hart geraten ist, wie schon Loriot wusste ("Berta – das Ei ist hart!").

Wer immer die gleiche Größe Eier im Laden kauft und sie zuhause für sich selber kocht, kennt seine Vorliebe und weiß inzwischen, wie lang das Ei kochen muss. Aber was, wenn man Besuch bekommt und der eine will es sehr weich, die nächste so mittel und die Kinder bekommen einen Schreianfall, wenn das kleinste bisschen glibbliges Material zu detektieren ist? Wenn dann noch erschwerend hinzukommt, dass die Eier nicht aus der Fabrik kommen, sondern von Nachbars Hühnern, die sich einen Scheiß um Größenklassen scheren, dann ist die Katastrophe perfekt!

Außerdem versteht es sich von selbst, dass man ein für die Menschheit so zentrales Problem, wie das Eierkochen nicht einfach seinem Gefühl überlassen kann! D.h. wir brauchen eine belastbare Lösung, die sich aus wissenschaftlichen Prinzipien ableiten lässt.

Wann ist das Ei perfekt?

Zunächst mal ist die Frage zu klären, wann ein Ei als perfekt anzusehen ist. Bei der Bewertung geht es darum, welche Konsistenz, Eiweiß und v.a. Eigelb haben. Dazu ziehen wir das Werk "Modernist Cuisine at Home" von Nathan Myhrvold und Maxime Bilet zu Rate. Im Kapitel Frühstückseier, das immerhin 12 Seiten umfasst, gibt er eine umfassende Übersicht der Eiertextur nach Kerntemperatur. Ich mag gerne weiche Eier, aber will kein flüssiges Eiweiß haben. Also dürfte mein Geschmack so irgendwo zwischen 65 und 70°C getroffen werden.

Ein Weg zum perfekten Ei führt nun über den Weg des sous vide Garens. Dabei bringt man ein Wasserbad exakt auf die gewünschte Zieltemperatur und legt das Ei für eine gefühlte Ewigkeit in selbiges. Am Ende hat das gesamte Ei die gewünschte Temperatur. Das habe ich tatsächlich schonmal so gemacht und ein perfektes 68°C Ei genossen. Es war super – aus irgendwelchen Gründen hat das 45 Minuten Ei aber keinen dauerhaften Einzug in unser Küchenrepertoire gehalten.

Wer sich dafür interessiert sei auf die Seiten von Modernist-Cuisine oder Serious Eats verwiesen.

Technologie zu Hilfe!

Nun gibt es im Appstore Eures Vertrauens so tolle Eierkochtimerapps – ich hab auch mal eine runtergeladen und sie funktioniert ganz gut. Meine Frühstückseiproduktion hat merklich an Konsistenz gewonnen, auch wenn besagte Nachbarshühner grade mal Lust hatten, 32g Eier zu legen. Aber wer will schon eine App? Da muss ja eine Formel dahinter stehen und die will ich wissen!

Science!

Eine kurze Google Suche führte mich zu einem Artikel von Charles D. H. Williams, Lecturer am Department of Physics and Astronomy der University of Exeter.

Williams erklärt hier die Physik hinter dem Eierkochen. Um die Erwärmung des Ei-Inneren zu berechnen macht er ein paar vereinfachende Annahmen, wie z.B. dass das Ei kugelförmig sei. Das sollte zulässig sein. Um das perfekte Ei zu kochen brauchen wir zunächst ein paar Variablen, die das System definieren:

M: Masse [g]
T₀: Starttemperatur [K]
T₁: Zieltemperatur [K]
T_w: Wassertemperatur [K]

Dabei wird angenommen, dass T_w während des Kochvorgangs konstant bleibt. Also lieber den großen Topf mit viel Wasser nehmen, damit das näherungsweise stimmt. Auch ist zu berücksichtigen, dass T₁ bei Williams die Temperatur an der Eiweiß-Eigelb-Grenze ist. D.h. man benötigt etwas höhere Zielwerte, als beim sous vide. Neben diesen Variablen sind noch folgende Parameter zu berücksichtigen:

ρ: Dichte
r: Eigelb zu Eiweißverhältnis
c: spezifische Wärmekapazität
K: Wärmeleitfähigkeit

Letztlich gibt er die folgende Formel an:

$$ t_{\rm cooked} = \lambda \cdot M^r \cdot \log_e \left ( 0.76 \cdot \frac{ T_{0} - T_{w} }{ T_{1} - T_{w} } \right ) $$

Wobei

$$ \lambda = \frac{c \rho^{1-r}}{K \pi^2 ( 4 \pi / 3 )^r}$$

Die Werte für ρ, c und K entnimmt Williams der Literatur und postuliert r=2/3. Am Ende kommt er auf λ=27 für Eigelb, λ=31 für Eiweiß. Aufgrund oben genannter T₁ Definition sind also hier die Werte für Eiweiß und nicht Eigelb einzusetzen.

Der Physiker gibt Temperaturen immer in Kelvin (K) an. Da in der Formel aber nur Temperaturdifferenzen vorkommen und die Kelvin- und Celsiusskala sich nur durch den Wert des Nullpunkts unterscheiden, können genausogut Celsiuswerte verwendet werden. Nur wenn man obskure Temperatureinheiten, wie Fahrenheit, Delisle oder Réaumur verwendet, muss zuvor umgerechnet werden.

Die Kochzeit unseres Eis hängt also wie folgt von der Größe ab:

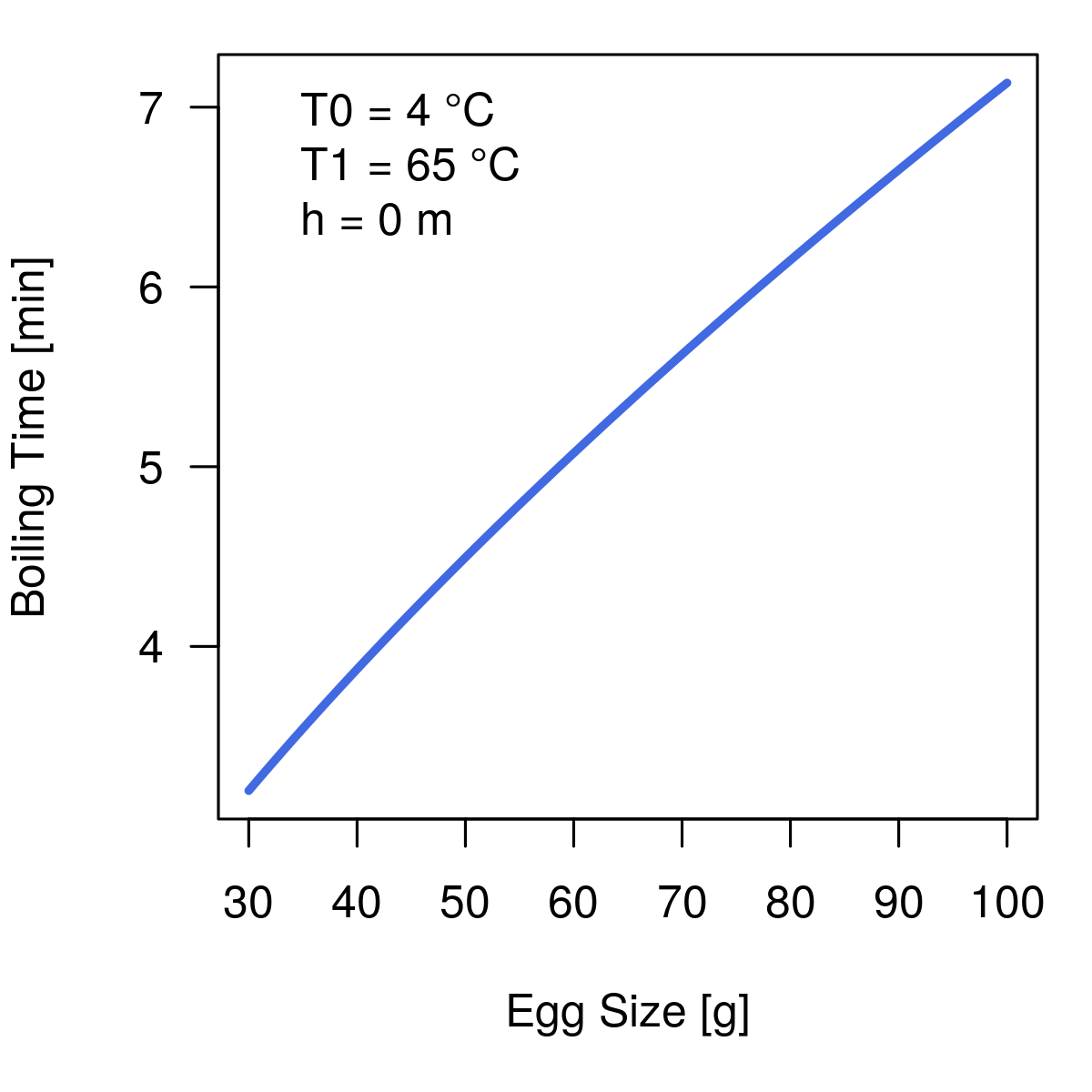
Aber welchen Einfluß haben die Start- bzw. Zieltemperatur? Diesen:

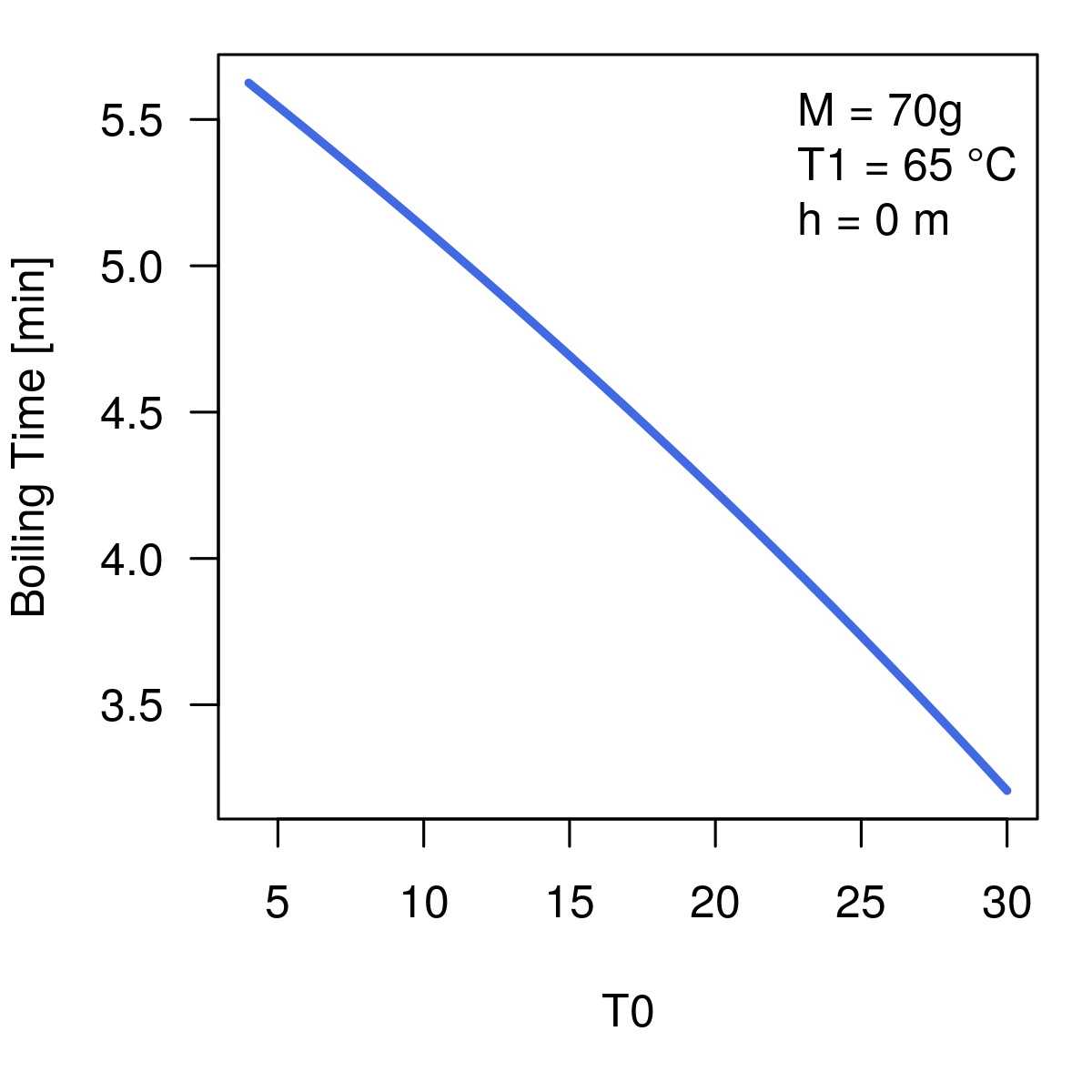
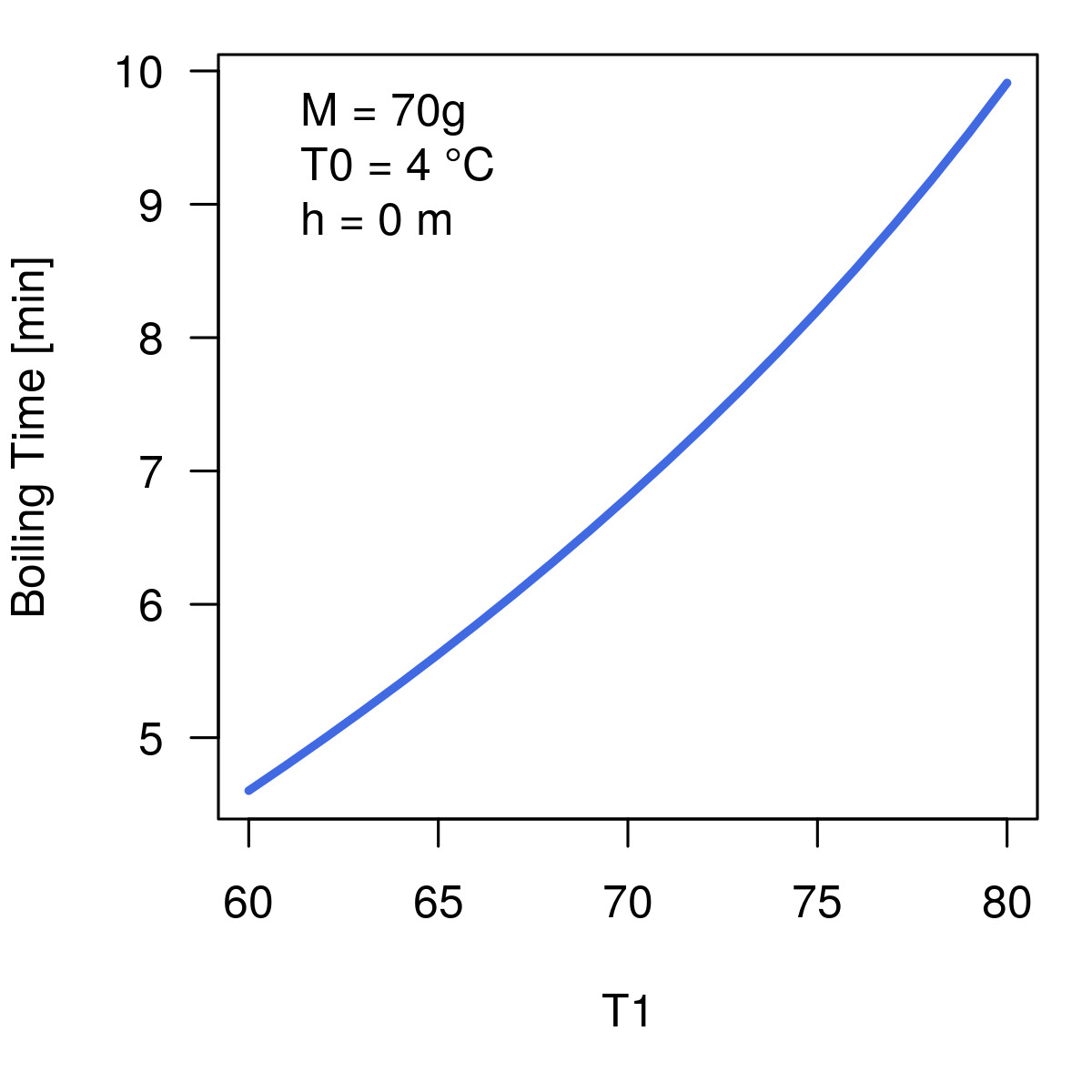
Der Unterschied zwischen einem Ei aus dem Kühlschrank und einem bei Raumtemperatur macht also hier mehr als eine Minute aus – hätte ich nicht erwartet!

Für Küstenbewohner ist das Problem damit gelöst, denn die Kochtemperatur T_w = 100°C = 373.15K. Aber wenn das Ei der Begierde zufällig auf einer Berghütte zubereitet werden soll, dann ist auch das zu berücksichtigen, denn der Siedepunkt des Wassers hängt vom Luftdruck ab und der nimmt mit zunehmender Höhe deutlich ab. Dazu kann man die Clausius–Clapeyron Gleichung verwenden:

$$ \log_e \frac{p_0}{p_1} = \frac{-H_{mv}}{R} \cdot \left ( \frac{1}{T_0} - \frac{1}{T_1} \right )$$

p₀: Druck im Zustand 0 (1013.25 hPa)
p₁: Druck im Zustand 1
T₀: Temperatur im Zustand 0 (100 °C = 473.15 K)
T₁: Temperatur im Zustand 1
H_mv: molare Verdampfungsenthalpie [J/mol]
R: allgemeine Gaskonstante (8.314 J/(K * mol))

Achtung: T₀ in dieser Gleichung ist nicht das gleiche, wie T₀ in der obigen Formel! Tatsächlich geht es hier um das was oben T_w hieß. Zudem muss hier wirklich in Kelvin gerechnet werden.

p₀ und T₀ sind bekannt (Standardbedingungen) und p₁ ist gegeben durch die Höhe oder den gemessenen Luftdruck. Gesucht ist T₁ – und danach müssen wir nun auflösen:

$$ \begin{align*} \log_e \frac{p_0}{p_1} & = - \frac{H_{mv}}{R} \cdot \left ( \frac{1}{T_0} - \frac{1}{T_1} \right ) \\ \log_e \frac{p_0}{p_1} & = - \frac{H_{mv}}{R \cdot T_0} + \frac{H_{mv}}{R \cdot T_1} \\ \log_e \frac{p_0}{p_1} + \frac{H_{mv}}{R \cdot T_0} & = \frac{H_{mv}}{R \cdot T_1} \\ \frac{\log_e \frac{p_0}{p_1} + \frac{H_{mv}}{R \cdot T_0}}{H_{mv}} & = \frac{1}{R \cdot T_1} \\ \frac{H_{mv}}{(\log_e\frac{p_0}{p_1} + \frac{H_{mv}}{R \cdot T_0}) \cdot R } & = T_1 \\ T_1 & = \frac{H_{mv}}{R \cdot \log_e\frac{p_0}{p_1} + \frac{H_{mv}}{T_0}} \\ \end{align*} $$

Die Gaskonstante ist klar, also fehlt uns noch die Verdampfungsenthalpie H_mv. Die ändert sich fieserweise mit der Temperatur. Das könnte man näherungsweise berechnen, aber wenn man die obige Formel verwendet, wird ohnehin davon ausgegangen, dass H_mv konstant ist. D.h. das funktioniert nur solange der Temperaturunterschied nicht sehr groß wird. Erfreulicherweise interessieren wir uns eh nur für den Temperaturbereich von ≈70 (Hochgebirge) bis 100 °C (auf Meereshöhe) in dem die Verdampfungsenthalpie ≈42 bis 40.657 kJ/mol beträgt (also max. 3.3% Fehler). Damit kann man leben und wir setzen H_mv = 40.657 kJ/mol.

Aber wie hoch ist die Druckänderung nach Höhe? Auch hier weiß Wikipedia Rat und gibt uns die Internationale Höhenformel, allerdings ist auch die nur eine Näherung:

$$ p(h) = 1013.25 \cdot \left ( 1- \frac{0.0065 \cdot h}{288.15} \right )^{5.255} $$

p(h): Luftdruck [hPa] in Höhe h
h: Höhe über Meeresspiegel [m]

Diesen Druck p(h) kann man nun als p₁ in die Gleichung für die Siedetemperatur einsetzen und schon hat man die Höhenkorrektur. Und so sehen Luftdruck und Siedetemperatur dann in Abhängigkeit der Höhe aus:

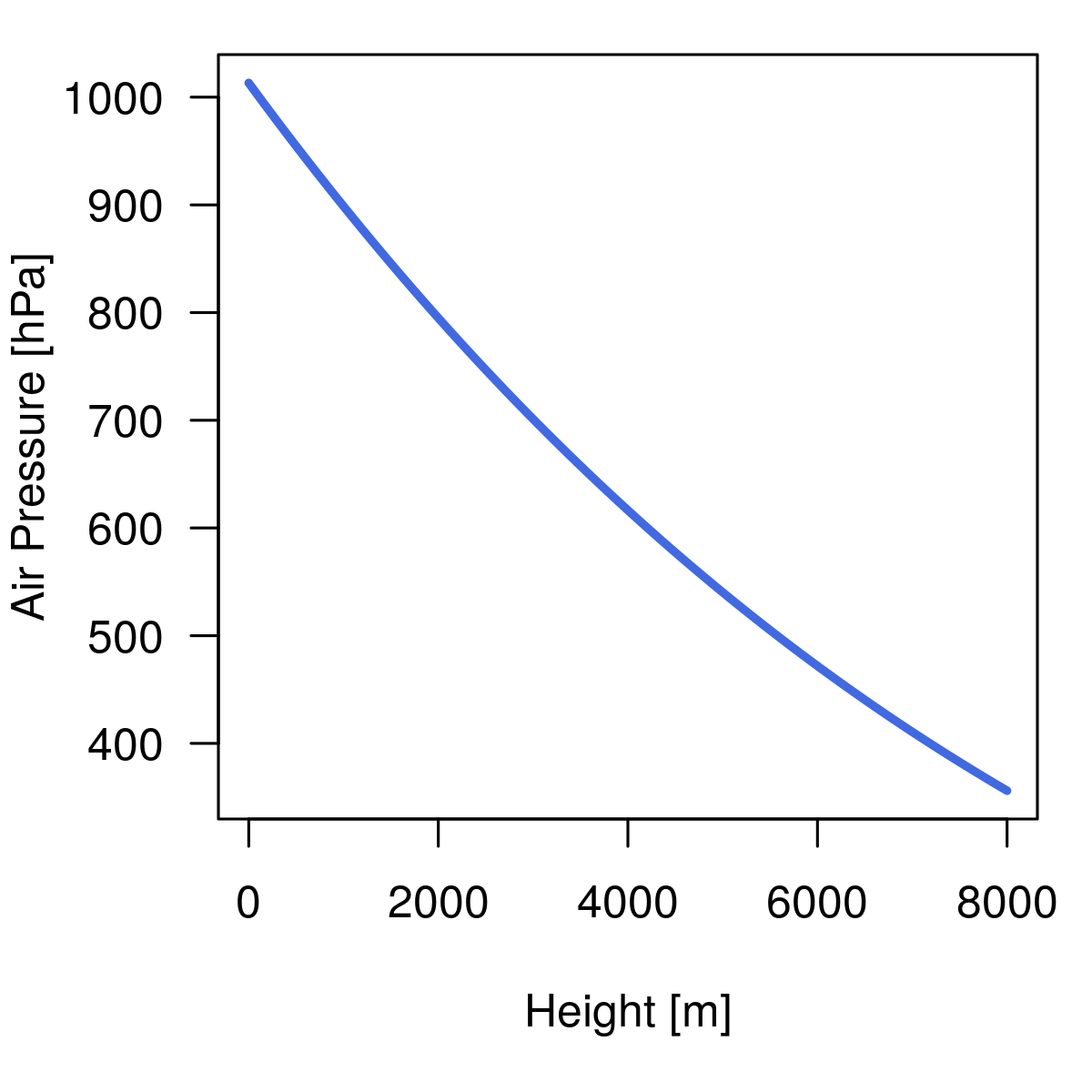
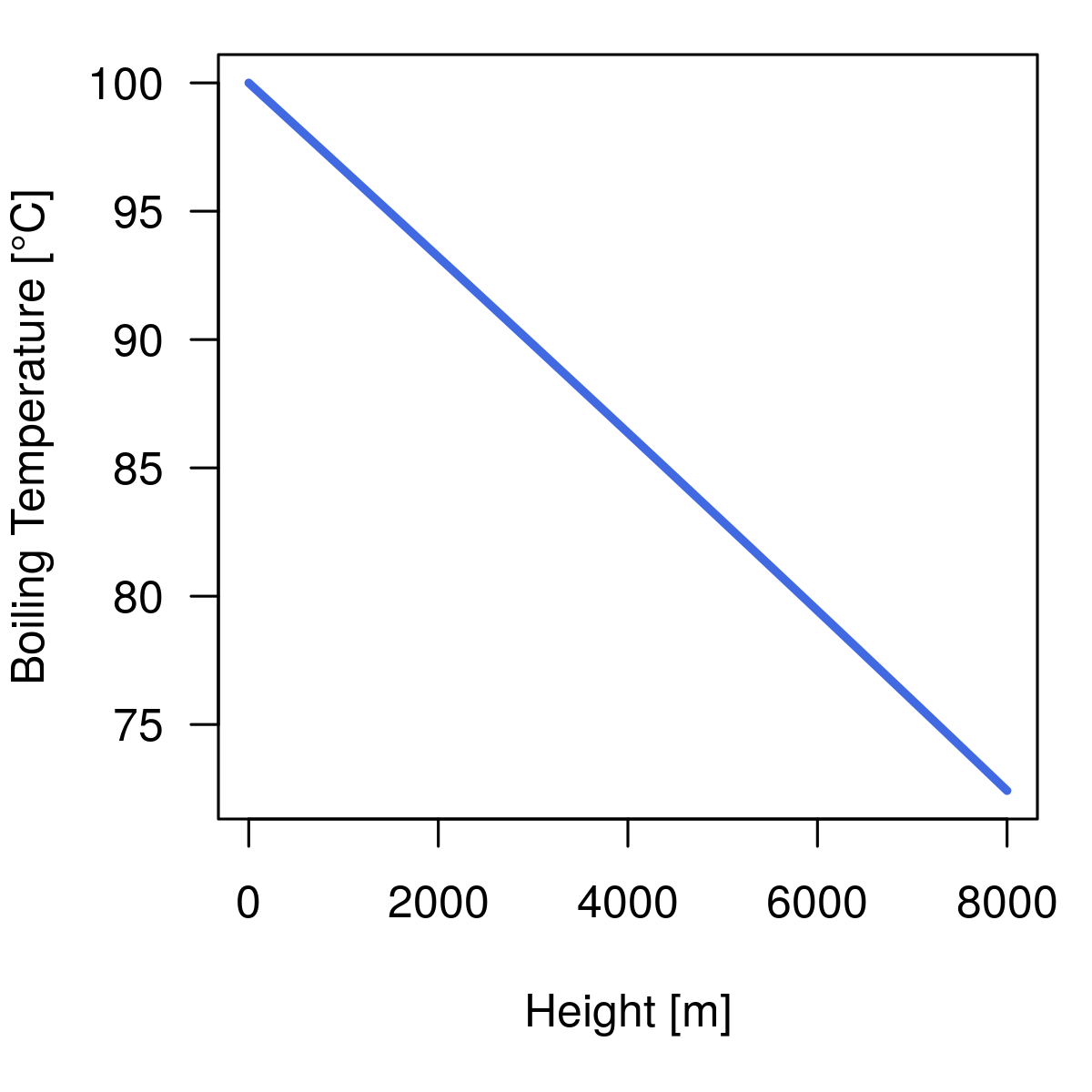
Nun können wir die Kochdauer für unser Ei berechnen oder graphisch darstellen:

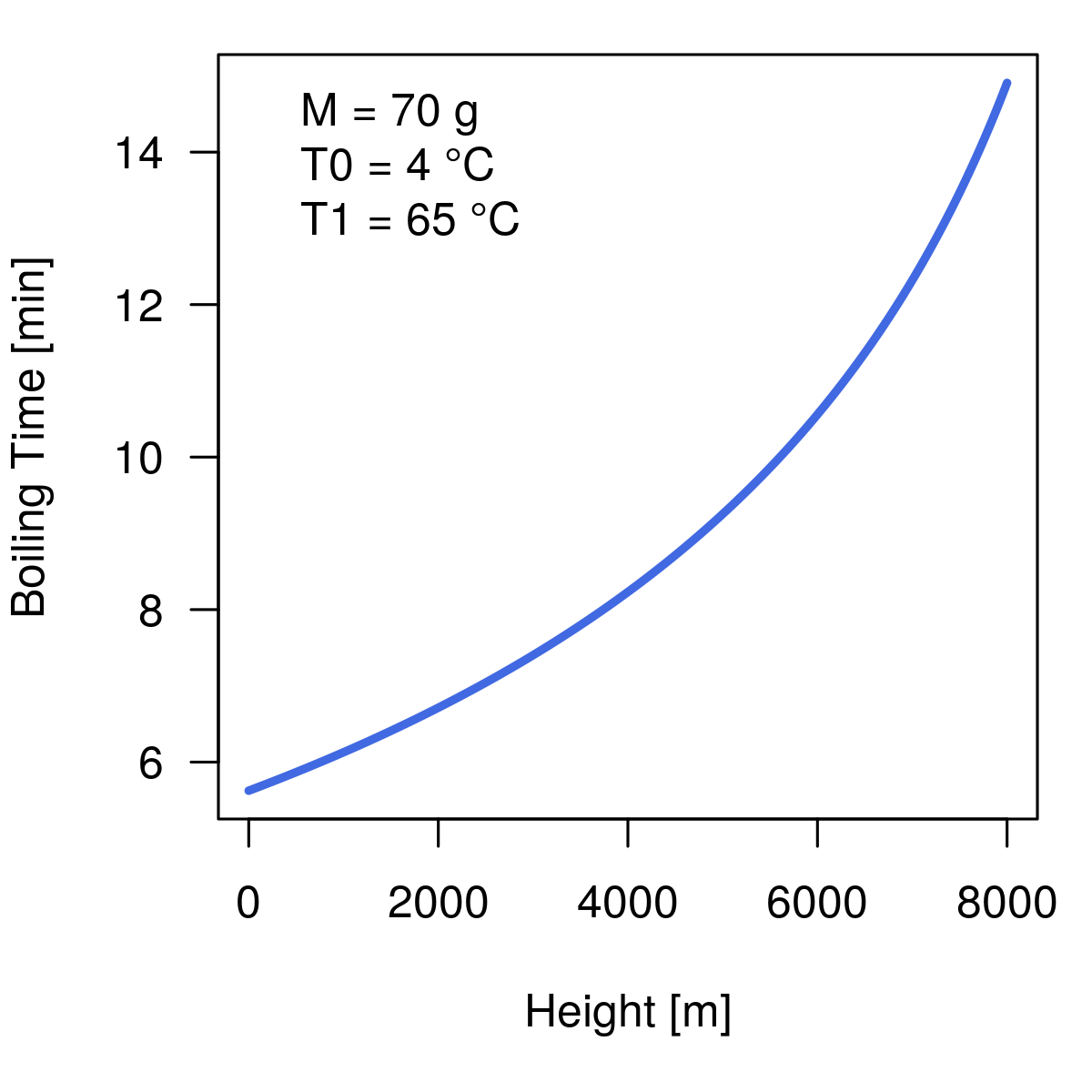
Wow – also auf einem Achttausender dauert das Frühstücksei mehr als doppelt so lang!

Implementierung

Nun muss ich das gelernte natürlich sofort in die Tat umsetzen. Also schnell in R schreiben:

BoilingTime <- function(M=70, T0=4.0, T1=65, h=0, r=2/3){
    # returns the boiling time [s] for the egg
    #
    # M:    mass [g]
    # T0:   egg temperature at time 0
    # T1:   target egg temperature
    # alt:  altitude [m]
    # r:    fraction of yolk compared to egg mass
    #
    # All temperatures in °C

    # set some parameters
    c <- 3.7        # specific heat capacity
    rho <- 1.038    # density
    kappa <- 5.4e-3 # thermal conductivity
    Hmv <- 40.657   # enthalpy of vaporization
    R <- 8.314      # gas constant
    P0 <- 1013.25   # pressure at sea level

    # compute boiling time
    TW <- boiltemp(h)
    lambda <- (c * rho**(1-r)) / (kappa * pi**2 * ( 4*pi/3 )**r)
    boiltime <- lambda * M**r * log(0.76 * (T0 - TW)/(T1 - TW))

    return(boiltime)
}

airpressure <- function(h=0){
    # return atmospheric pressure at altitude h [m]

    1013.25 * ( 1 - (0.0065 * h)/288.15)**5.255
}

boiltemp <- function(h=0){
    # return boiling temperature at altitude h [m]

    Hmv <- 40.657e3 # enthalpy of vaporization
    R <- 8.314      # gas constant
    T0 <- 373.15    # boiling temperature at sea level [K]
    P0 <- 1013.25
    P1 <- airpressure(h)

    T1 <- Hmv / (R * log(P0/P1) + Hmv/T0)

    T1 - 273.15
}

Wenn Euch das interessiert, kopiert Euch den obigen Code und spielt mal selber damit rum, oder verwendet ihn, um Euer Frühstücksei zu kochen...