Gefrierschrank Stromverbrauch
Posted on Fri 21 October 2022 in Science & Medicine
Energiesparen ist das Motto der Stunde. Vor allem bezieht sich das auf Erdgas, aber natürlich macht es Sinn, in allen Bereichen Energie zu sparen. Zum Einen weil es Geldbeutel und Umwelt schont, zum Anderen, weil man bei Gasmangel eben auch mit Strom Wärme erzeugen kann.
Und so sind die Medien und das Netz voll von Tipps zum Sparen. Smarte Thermostate, Raumtemperatur senken, mit Sand abreiben statt Duschen, richtig Lüften, Heizung warten lassen etc. etc. Aber welche Maßnahme ist wirklich sinnvoll? Und wieviel kann ich damit sparen?
Heute wollen wir uns mal eine Maßnahme herauspicken und untersuchen, was sie bringt: Wie ändert sich der Stromverbrauch eines Tiefkühlers, wenn wir die Solltemperatur ändern?
Der Prüfling
Ich habe im Hauswirtschaftsraum einen Tiefkühler von Liebherr stehen (GNP 1066-20). Als ich ihn gekauft hatte, war er in Energieffizienzklasse A++, durch die Reform der Klassen ist er heute in Kategorie E zu finden.
Der wird nur gelegentlich geöffnet und kühlt die Vorräte so vor sich hin. Ich habe mal nachgeschaut und aktuell ist er auf eine Solltemperatur von -20°C eingestellt. Das ist vermutlich kälter, als es sein muss. Im Netz habe ich ziemlich durchgehend die Empfehlung gelesen den Tiefkühler auf -18°C einzustellen, auch wenn das scheinbar alle nur voneinander abschreiben, denn keine Seite hatte eine vernünftige, nachvollziehbare Begründung zu bieten. Auch gab es zu der dort angegebenen Energieersparnis keinerlei Quellen, die man prüfen könnte. Also: selbst ist der Mann.
Experiment
Zuerst wollte ich unseren "Hauptkühlschrank" in der Küche verwenden (Kühl-/Gefrierkombi), aber der wird natürlich häufiger geöffnet und auch jeden Tag anders. Z.B. recht lange nach dem Einkauf, nur kurz an anderen Tagen. Das ist kein grundsätzliches Problem, aber es bedeutet, dass wir sehr viele Tage einbeziehen müssen, um trotz der Variabilität belastbare Daten zu bekommen. Deshalb nehmen wir den Tiefkühler im Hauswirtschaftsraum – der ist unser Langzeit-Vorrat und wird entsprechend nur selten geöffnet. Und so fällt es leicht, für die Auswertung eine Periode zu finden in der er garnicht geöffnet oder sonstwie manipuliert wurde.
Die Raumtemperatur um den Freezer ist recht konstant und wir werden sie ignorieren.
Fragestellungen:
- Gibt es einen signifikanten Unterschied im Energieverbrauch in Abhängigkeit der eingestellten Temperatur von -20°C vs. -18°C?
- Wenn ja – wie groß ist dieser Unterschied?
- Wie groß ist die Variabilität im Verbrauch?
Daten
Zunächst lassen wir den Freezer eine Weile in Ruhe bei -20°C laufen und zeichnen dabei den Energieverbrauch auf. Nach ein paar Tagen schalten wir dann auf -18 °C. Den Tag der Umschaltung streichen wir aus der Statistik, weil wir hier ja einen Übergangszustand haben.
Zuerst schauen wir uns mal an, wie der Energieverbrauch eines Tiefkühlers überhaupt strukturiert ist:
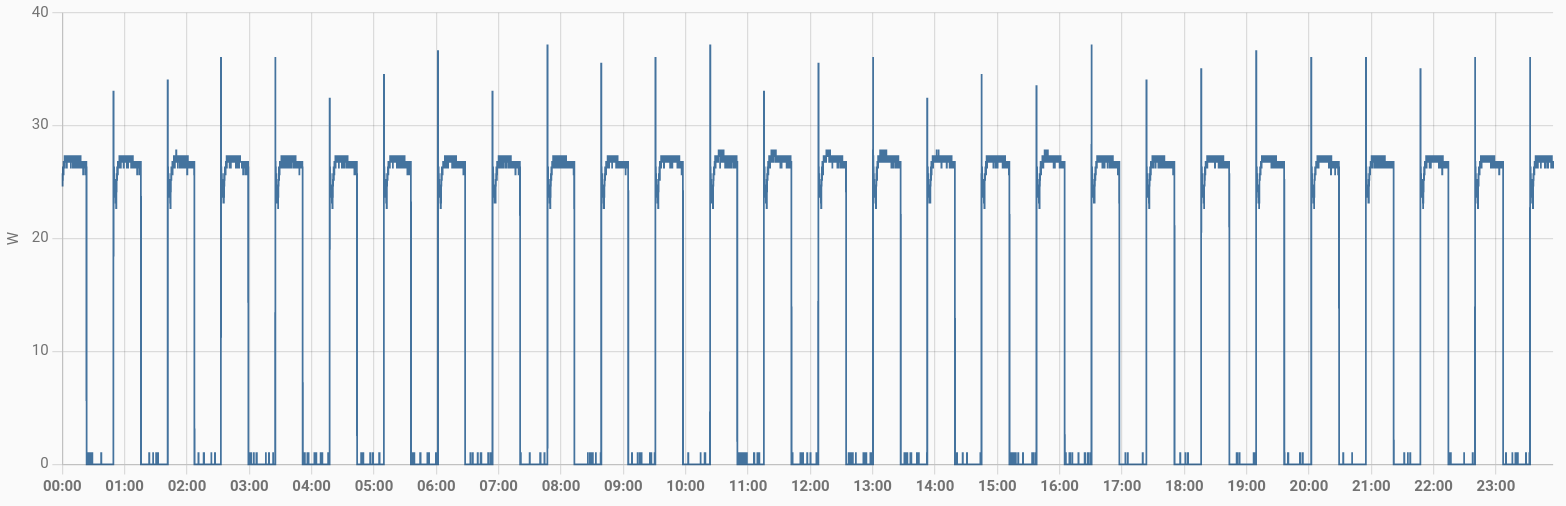
Wie man sieht, läuft der Kühlkompressor ca. die Hälfte der Zeit. Dabei verbraucht er so ca. 27W. In den Intervallen dazwischen verbraucht das Gerät keinen Strom.
Meine Messdaten decken den Zeitraum vom 4. bis 21.10. ab. Am 9.10. irgendwann zwischen 15:00 und 16:00 habe ich dann die Temperatur auf -18°C umgestellt (rote Line). Also schauen wir uns das mal an:
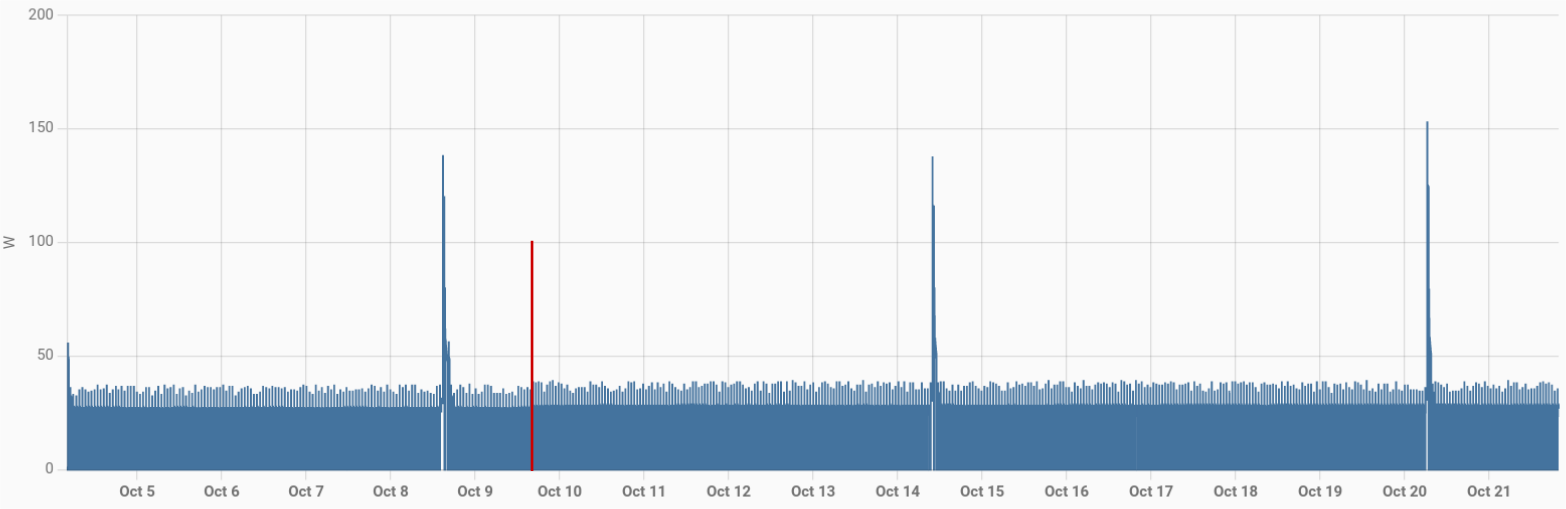
Als erstes fallen diese Verbrauchs-Spitzen auf. Ich vermute dass es sich dabei um die No-Frost Funktion handelt. Dabei heizt der Freezer kurzzeitig seinen Kühlkreislauf auf, um eventuelles Eis oder Reif wieder loszuwerden.
Einen Unterschied durch die Umstellung sieht man hier nicht, denn der Energieverbrauch beim Kühlen bleibt natürlich der gleiche – was sich verändert ist die Länge der Kühl-Intervalle. Das kann man tatsächlich mit bloßem Auge erkennen, wenn man sich nur den Tag der Umstellung anschaut:
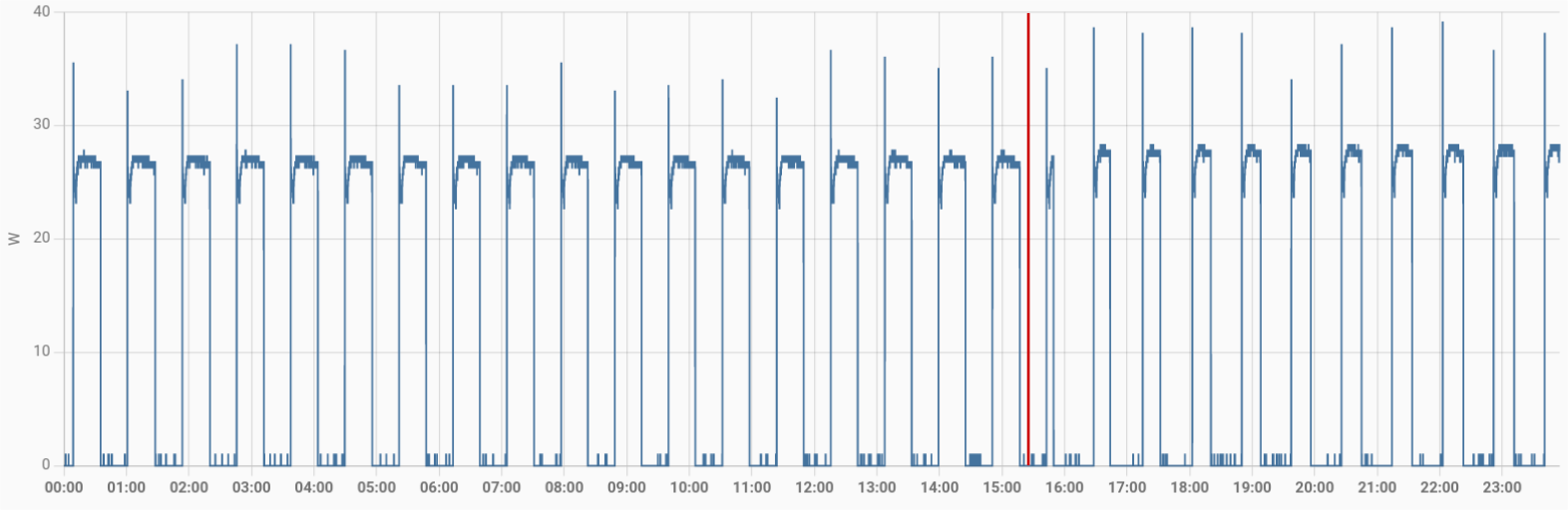
Um nun den Energieverbrauch zu beurteilen schauen wir uns mal an, wie sich der Tagesverbrauch verhält. Homeassistant summiert einfach den Verbrauch im Laufe des Tages auf und setzt ihn dann um Mitternacht wieder auf 0 und das Spiel beginnt von neuem:
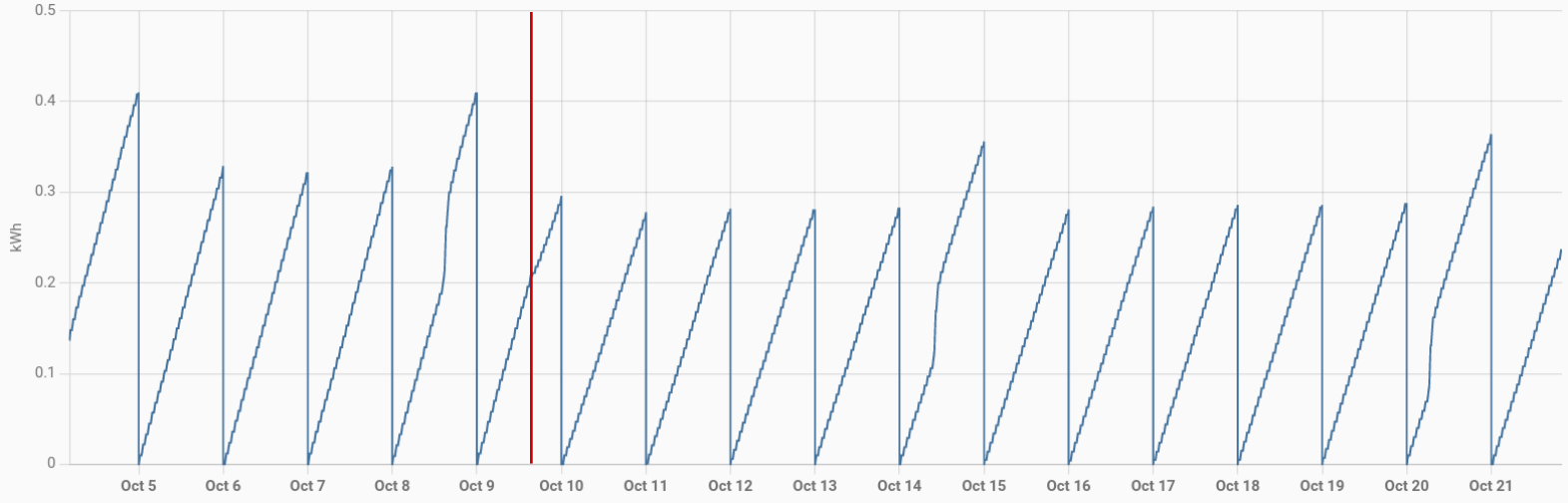
Wenn wir die Tage mit No-Frost Aktivität, sowie den der Umstellung ignorieren, dann bekommen wir folgende Zahlen:
| Temperatur | Tagesverbrauch [kWh] |
|---|---|
| -20°C | 0.33 |
| -20°C | 0.32 |
| -20°C | 0.33 |
| -18°C | 0.28 |
| -18°C | 0.28 |
| -18°C | 0.28 |
| -18°C | 0.28 |
| -18°C | 0.28 |
| -18°C | 0.28 |
| -18°C | 0.29 |
| -18°C | 0.29 |
| -18°C | 0.29 |
Also sinkt der Verbrauch auf \(0.28 / 0.33 = 84.9\%\). Ich spare also rund 15% Energie. Das ist durchaus respektabel. Und statistisch signifikant ist es auch:
> V20 = c(0.33, 0.32, 0.33)
> V18 = c(.28, 0.28, 0.28, 0.28, 0.28, 0.28, 0.29, 0.29, 0.29)
> t.test(V20, V18, alternative="greater")
Welch Two Sample t-test
data: V20 and V18
t = 11.628, df = 3.0769, p-value = 0.0006061
alternative hypothesis: true difference in means is greater than 0
95 percent confidence interval:
0.03465154 Inf
sample estimates:
mean of x mean of y
0.3266667 0.2833333
Also \(p=\)0.0006061
An den Tagen mit no-frost bekommen wir \(0.36/0.41 = 87.8\%\). Es scheint auch, dass der Abstand zwischen den no-frost Aktivitäten größer wird, aber wir haben nicht genug Daten, um das wirklich behaupten zu können.
Und zuguterletzt beantworten wir noch die Frage nach der Variabilität im Verbrauch. Wie wir oben gesehen haben ist die Variabilität bei konstanten Bedingungen so gut wie null. Nur die No-Frost Aktivität bringt Variabilität rein. Um also eine realistischere Idee für die Variabilität im normalen Alltag zu bekommen schauen wir uns an, wie sich der Stromverbrauch der Kühl-Gefrierkombi in der Küche im gleichen Zeitraum verhalten hat:
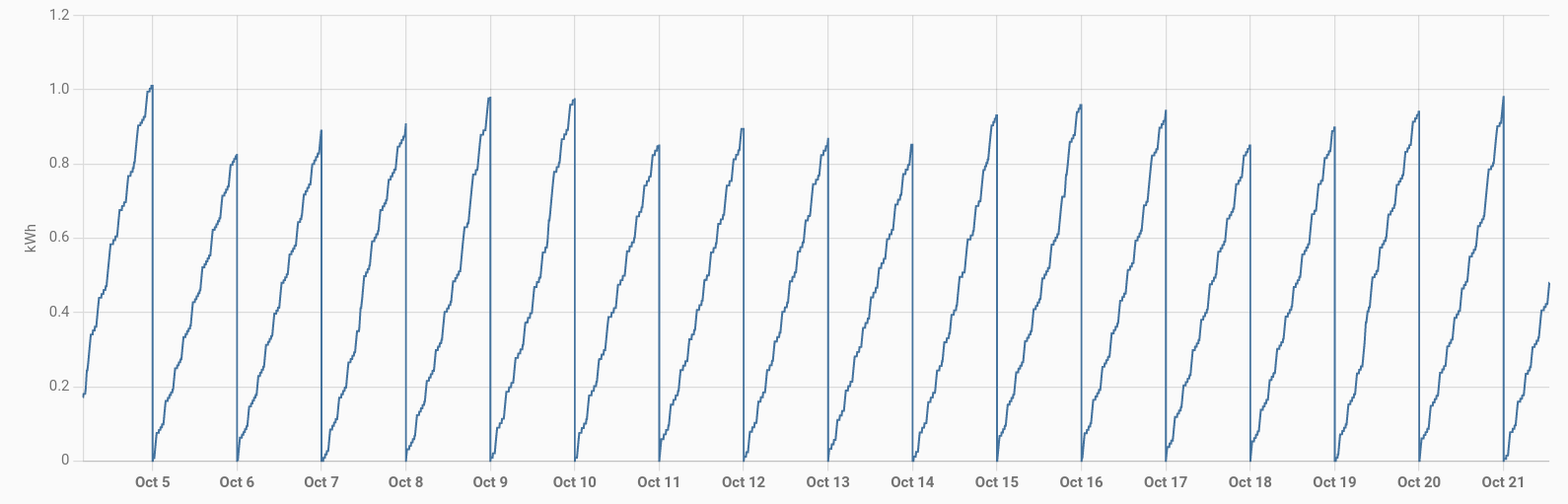
Unser Datensatz ist nicht besonders groß, aber für eine grobe Orientierung sollte es reichen. Also rechnen wir mal ein paar Kennzahlen aus:
> Vkombi = c(1.01, 0.82, 0.89, 0.91, 0.98, 0.98, 0.85, 0.90, 0.87, 0.85, 0.93, 0.96, 0.95, 0.85, 0.90, 0.94, 0.98)
> max(Vkombi) - min(Vkombi)
[1] 0.19
> mean(Vkombi)
[1] 0.9158824
> sd(Vkombi)
[1] 0.05624265
> sd(Vkombi)/mean(Vkombi) * 100
[1] 6.140816
Der Variationskoeffizient liegt also bei ca 6%. Das hängt aber alles natürlich extrem vom konkreten Nutzungsverhalten ab: Wie oft wird die Tür geöffnet? Für wie lang? Welche Temperatur haben die Lebensmittel beim einräumen? Wieviel (Masse) Lebensmittel werden jeweils hinein gegeben und heraus geholt? Etc.
Modell
Als letztes möchte ich noch wissen, wie der Zusammenhang von Temperatur und Stromverbrauch aussieht. Ist er linear? Oder quadratisch?
Dazu brauchen wir erstmal mehr Daten. Also habe ich noch ein paar weitere Temperaturen eingestellt und den Verbrauch gemessen. Und so decke ich nun den Bereich [-22, -14] in Schritten von 2°C ab:
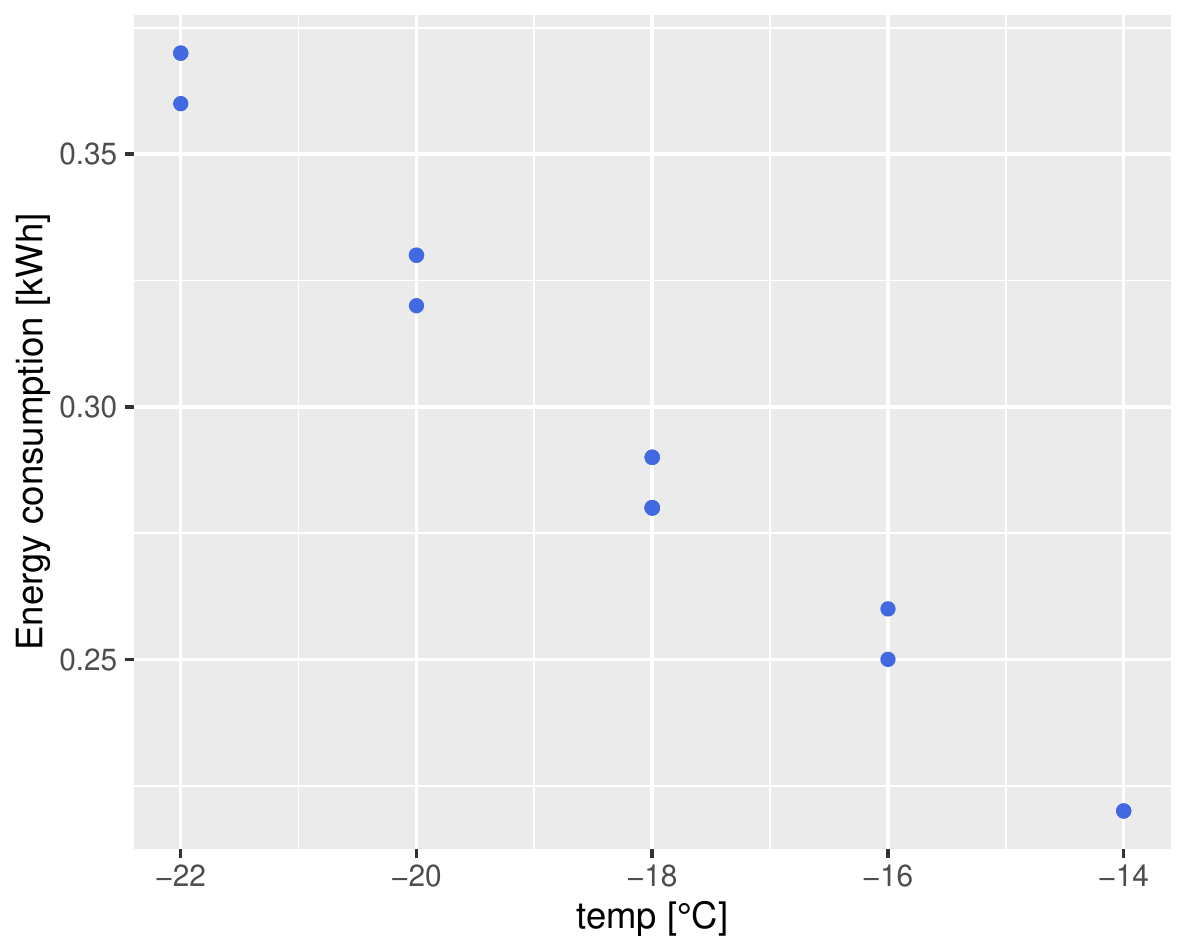
So vom Hinschauen könnte das eine Gerade sein, aber irgendwie schaut es leicht gekrümmt aus. Also testen:
# lineares Modell fitten
model1 = lm(consumption~temp, dat)
# quadratisches Modell fitten
model2 = lm(consumption~poly(temp, 2), dat)
# Und testen, ob es einen signifikanten Unterschied gibt
anova(model1, model2)
Analysis of Variance Table
Model 1: consumption ~ temp
Model 2: consumption ~ poly(temp, 2)
Res.Df RSS Df Sum of Sq F Pr(>F)
1 17 0.00075644
2 16 0.00047141 1 0.00028503 9.6742 0.006732 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
D.h. das quadratische Modell (\(\textit{consumption} = 0.01688 \cdot t^2 - 0.18354 \cdot t + 0.29368\)) passt signifikant besser. Das passt auch zum visuellen Eindruck:
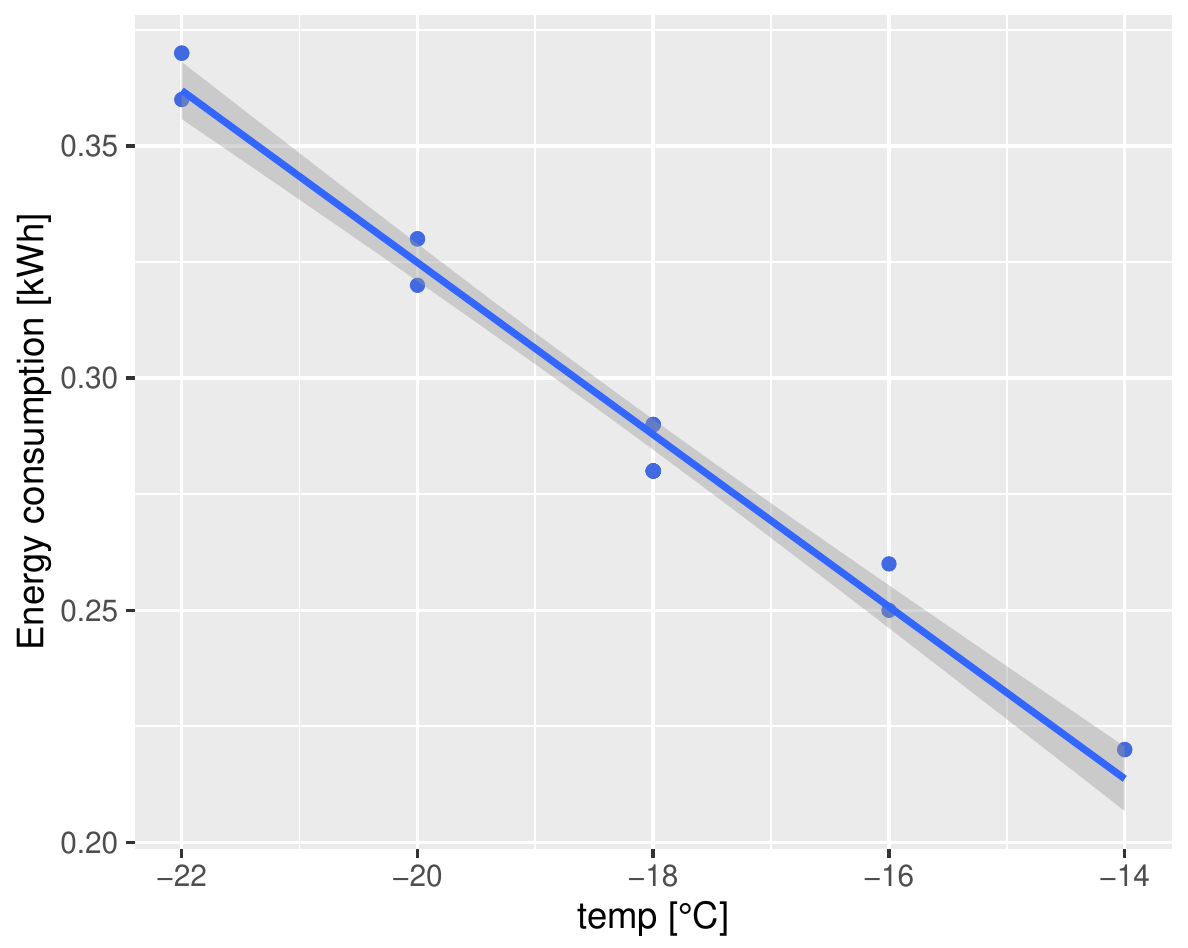
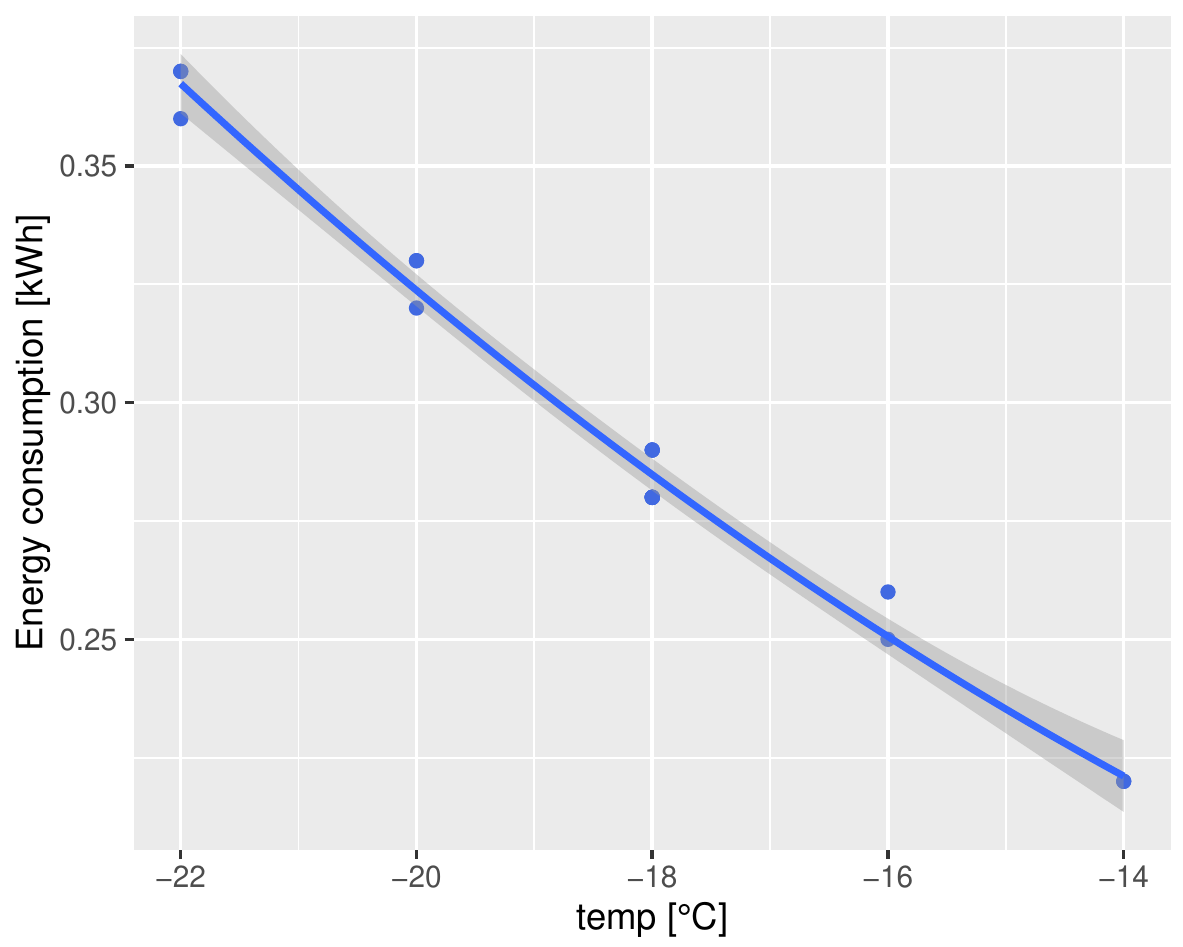
Und für Liebhaber von einfachen aber effektiven Experten-Lösungen bekommt Ihr auch noch die Augen-Zukneif-Methode, die ganz ohne Statistik funktioniert:

Fazit
Zwei Grad Unterschied bewirken tatsächlich eine spürbare Änderung des Energieverbrauchs. Und wir haben nun selbst gemessene Zahlen und müssen nicht blind glauben, was die ganzen Internetseiten so behaupten, also hat sich das Ganze schon gelohnt.