Power Sensor-Kalibrierung
Posted on Mon 22 August 2022 in Computer & Electronics
Smartplugs sind eine der wichtigsten Stützen in der Heimautomatisierung und so richtig Fahrt aufgenommen hat das mit den WLAN-Steckdosen von SONOFF, die so mit die ersten waren, für die es open source Firmware gab: TASMOTA. Heute gibt es diese Art smarte-Steckdosen wie Sand am Meer und mit Firmware-Alternativen wie ESPeasy, ESPurna und ESPhome stehen dem geneigten Maker jede Menge Optionen offen. Einige Modelle sind nicht nur schaltbar, sondern messen auch gleich den Stromverbrauch.
Und neuerdings habe ich ein paar davon und würde dieses Feature gerne nutzen. Das konkrete Modell heißt NOUS A1T und ist gegen einen kleinen Aufpreis bereits mit TASMOTA Firmware erhältlich, was einem das initiale Flashen erspart. Ja – das klingt unsportlich, aber der chinesische OEM dieser Dinger macht normalerweise seine Tuya Firmware drauf und es gibt ein lustiges Hase und Igel Spiel zwischen Tuya und dem OTA flashing tool, das es ein wenig zum Glücksspiel macht, ob die jeweiligen Smartplugs sich nun umflashen lassen, oder nicht.


Also erstmal einstecken, ins heimische WLAN einbinden und schauen, was das Ding so anzeigt:

Hm – 265V sind ein bisschen viel. Das stimmt nie im Leben. Und tatsächlich sagt mein Multimeter 228V:

Das schreit danach, die angezeigten Werte einmal systematisch zu überprüfen und eine Kalibrierkurve daraus abzuleiten.
Kalibrierkurve erheben
Ähnlich, wie für meinen Rangefinder, wollen wir nun also die Messwerte unseres Smartplugs mit einigermaßen vertrauenswürdigen Referenzwerten vergleichen. Die resultierende Kurve kann dann dazu genutzt werden, richtigere Werte zu bekommen – das nennt man Kalibrierung.
Unsere Referenz ist in diesem Fall ein Voltcraft-Energy-Monitor 4500advanced:

Das ist zwar auch kein Präzisionsinstrument, aber für den Hausgebrauch garnicht nicht übel. D.h. wenn wir unseren Smartplug so kalibieren können, dass er mit diesem Instrument übereinstimmt sind meine Anforderungen erfüllt.
Die folgenden Werte kann ich mit beiden Geräten messen:
- Spannung [V] (voltage)
- Strom [A] (current))
- Leistung [W] (power)
- Leistungfaktor (Power Factor)
Die wollen wir nun vergleichen und kalibrieren.
Unser Versuchsaufbau sieht so aus, dass wir das Energiemessgerät in die Steckdose stecken, den Smartplug in das Energiemessgerät und dann verschiedene Verbraucher in den Smartplug.

Wie man sieht, zeigt der Energiemonitor hier schon 0.8W an – das ist der Verbrauch des Smartplugs. Allerdings pendelt der sich über ein paar Minuten hinweg irgendwo zwischen 0.3 und 0.8W ein und so niedrige Level sind sicher auch nicht die Stärke meines eher günstigen Energiemonitors.
Damit das Ganze aussagekräftig ist werden wir versuchen, einen möglichst breiten Bereich von Leistung abzudecken und die jeweils angezeigten Werte beider Instrumente aufschreiben. Also habe ich mir einige Haushaltsgeräte geschnappt und deren Leistung vermessen. Hier die Ergebnistabelle:
load voltage current power pf voltage.sp current.sp power.sp pf.sp
1 Electric kettle 217.4 8.690 1900.0 0.99 252 7.798 1939 0.99
2 Hairdryer low cold 223.4 1.375 278.0 0.90 259 1.228 284 0.89
3 Hairdryer high cold 222.8 2.417 538.4 0.99 258 2.163 550 0.98
4 Hairdryer low warm 222.2 2.890 585.0 0.91 258 2.583 598 0.90
5 Hairdryer high warm 221.0 5.184 1146.0 0.99 256 4.634 1172 0.99
6 Hairdryer low hot 221.7 4.040 886.0 0.98 257 3.615 906 0.98
7 Hairdryer high hot 220.0 7.810 1719.0 0.99 255 6.991 1758 0.99
8 Kitchen radio 223.8 0.030 2.8 0.42 260 0.023 2 0.42
9 Mixer low 224.0 0.260 25.0 0.45 260 0.220 22 0.43
10 Mixer medium 223.0 0.240 47.0 0.88 259 0.211 47 0.86
11 Mixer high 223.0 0.330 76.0 0.99 259 0.290 77 0.99
12 Heater1 high 219.2 6.680 1450.0 0.99 254 5.940 1509 0.98
13 Heater1 low 220.3 4.250 931.0 0.99 256 3.811 955 0.98
14 Heater2 high 221.7 12.520 2786.0 0.99 257 11.235 2854 0.99
15 Vacuum cleaner full power 224.0 7.536 1642.0 0.97 260 6.742 1680 0.96
Der erste Satz Werte stammt vom Energie-Monitor, der zweite (*.sp) vom
Smartplug. Um die Daten besser zu verstehen plotten wir sie erstmal –
Referenzwerte auf der x-Achse und Smartplug-Werte auf der y-Achse. Die blaue
Line ist die Regressionsgerade, das graue Band das 95% Konfidenzintervall für
die Gerade und die rote gestrichelte Line kennzeichnet optimale Übereinstimmung:
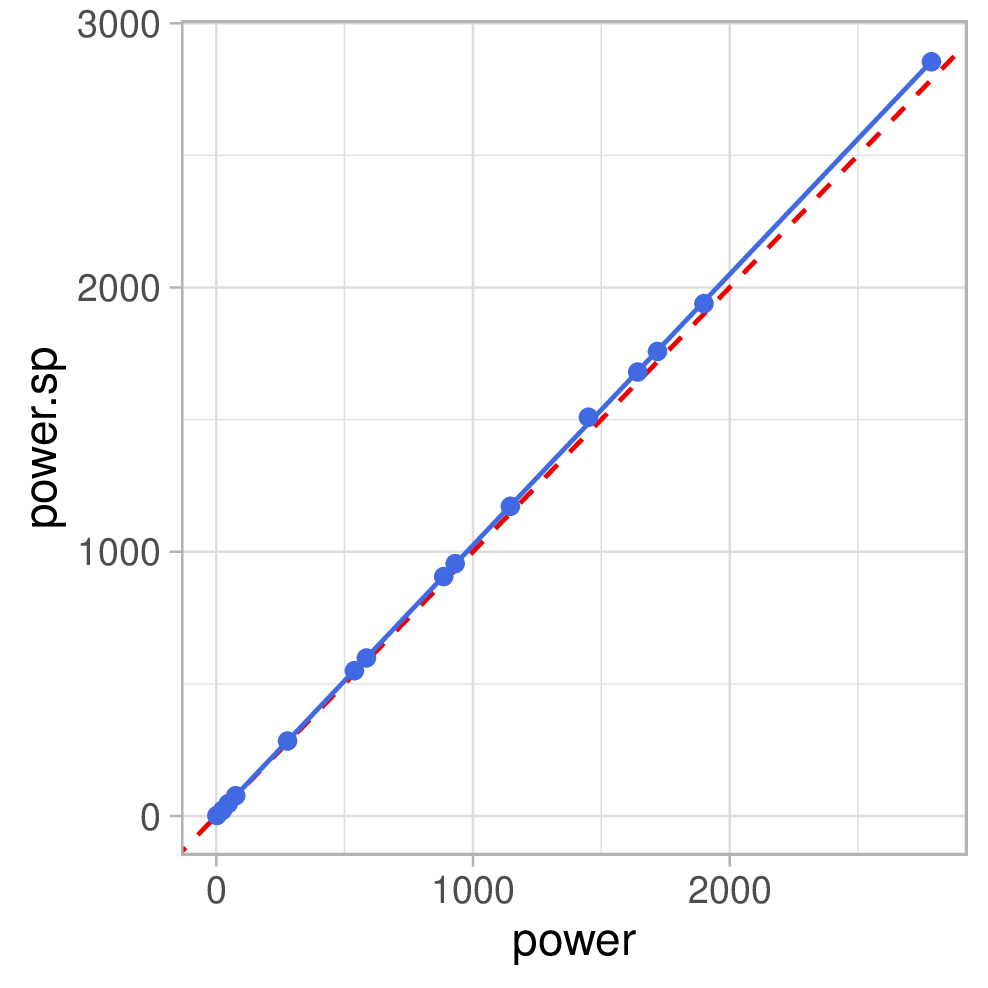
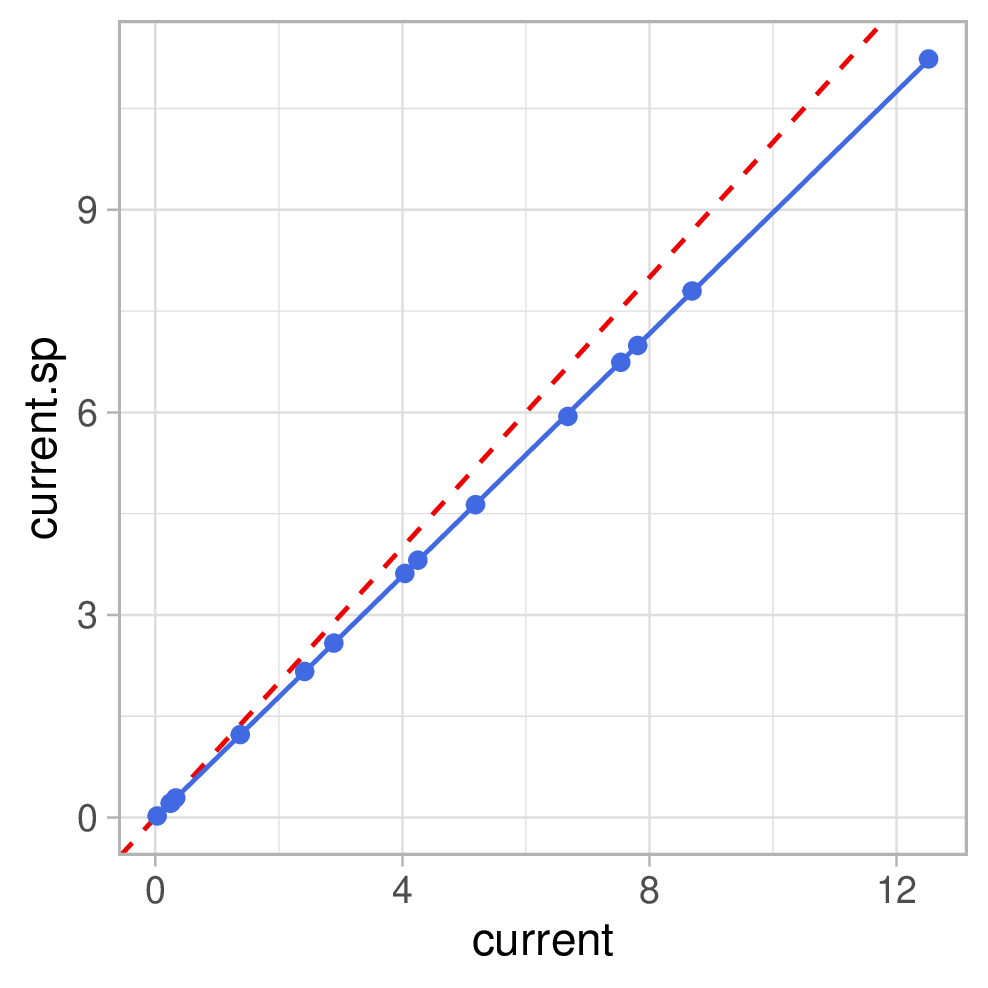
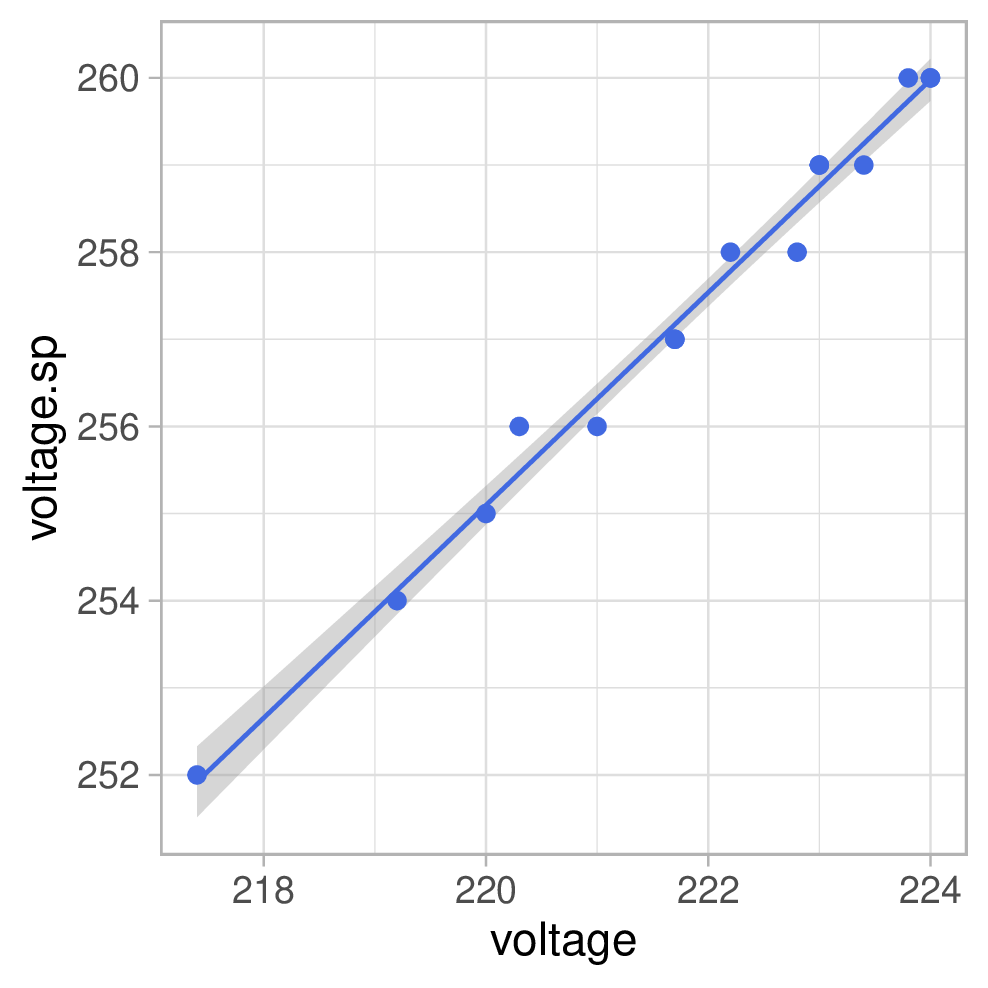
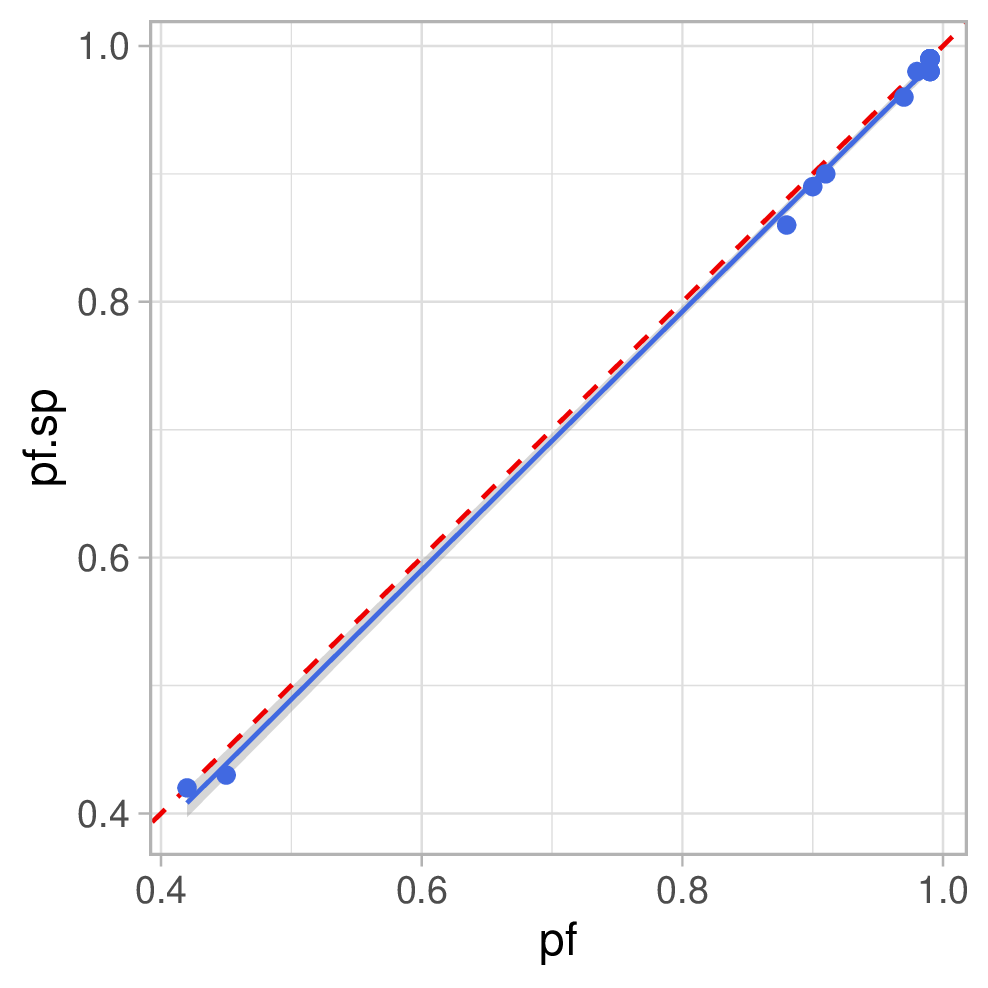
Wie man sieht, korrelieren die Messwerte sehr gut. Teils stimmen auch die absoluten Werte schon gut überein. Aber in manchen Fällen gibt es eine deutliche systematische Abweichung – v.a. die Spannungswerte sind völlig daneben. Naturgemäß decken wir hier nur einen recht kleinen Spannungsbereich ab, da die Netzspannung einigermaßen stabil ist und sich durch die Belastung mit einem Verbraucher auch nur minimal verändert. Wenn wir das genauer untersuchen wollten müssten wir einen regelbaren Trafo (Variac) verwenden, um von den bei uns üblichen 230V ernsthaft weg zu kommen. Ich würde vermuten, dass der Plug mindestens bis runter auf 100V funktioniert, denn 120V sind in den USA gebräuchlich.
Die Korrelationskoeffizienten lauten:
- Leistung (P): \(r = 0.9999684\)
- Strom (I): \(r = 0.9999922\)
- Spannung (U): \(r = 0.9934328\)
- Power Factor (λ): \(r = 0.9993514\)
Und die Gleichungen der Regressionsgeraden lauten:
- \(P_{sp} = 1.0253 \cdot P - 0.8815\)
- \(I_{sp} = 0.896767 \cdot I - 0.009003\)
- \(U_{sp} = 1.221 \cdot U - 13.484\)
- \(λ_{sp} = 1.01067 \cdot \lambda - 0.01622\)
Es fällt auf, dass alle Geraden fast exakt durch den Nullpunkt gehen. Und das macht auch Sinn: Außer für die Spannung wissen wir, dass bei fehlendem Verbraucher auch 0W und 0A angezeigt werden. Ohne Spannung funktioniert der Plug natürlich nicht, aber ich denke, wir können davon ausgehen, dass auch die Spannungskurve durch Null geht.
Ohne Intercept
D.h. wir sollten unsere Regressionsgerade ohne Intercept berechnen. So sehen dann die Plots aus:
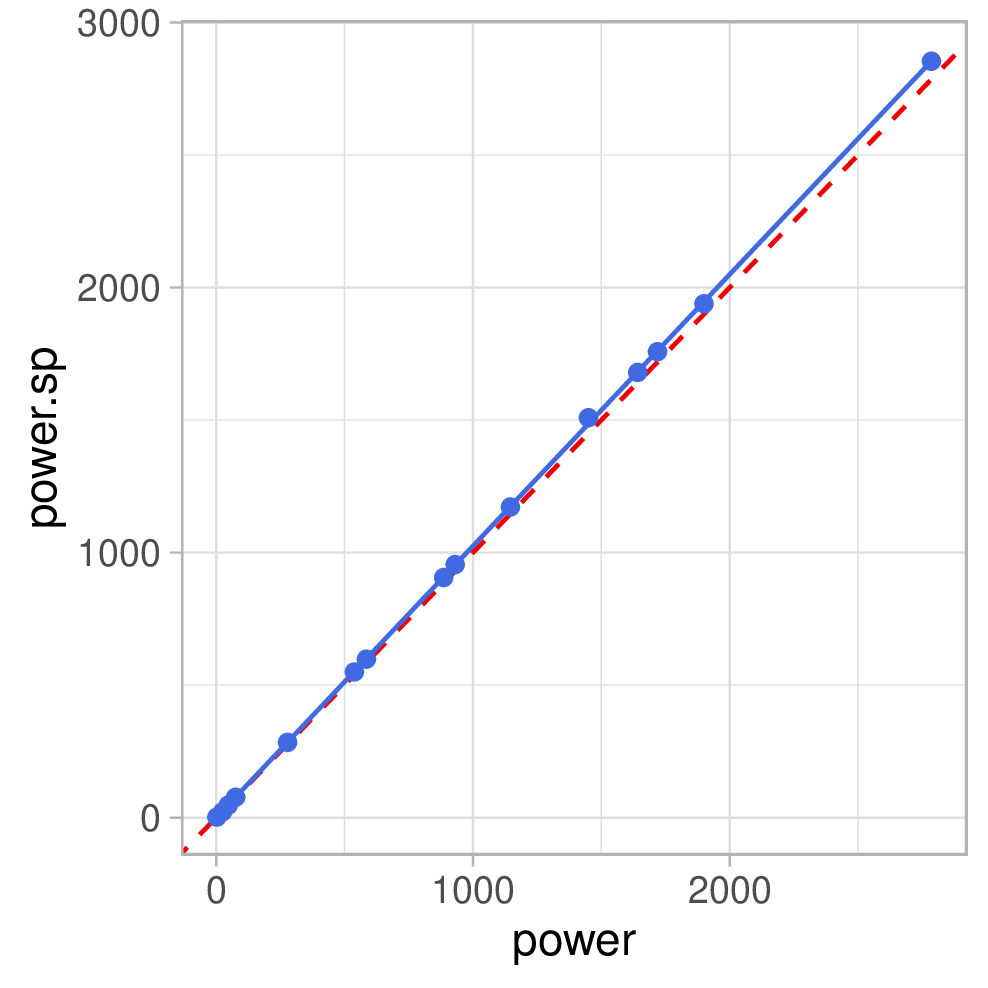
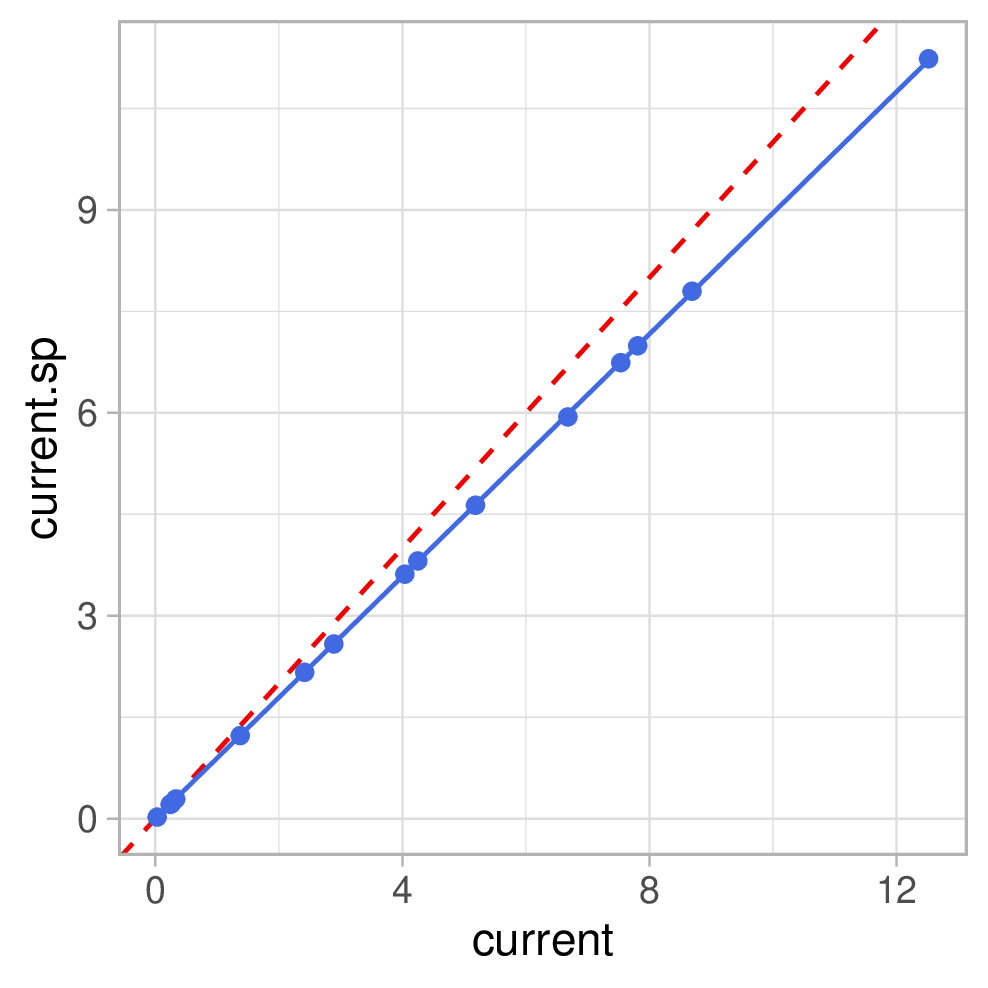
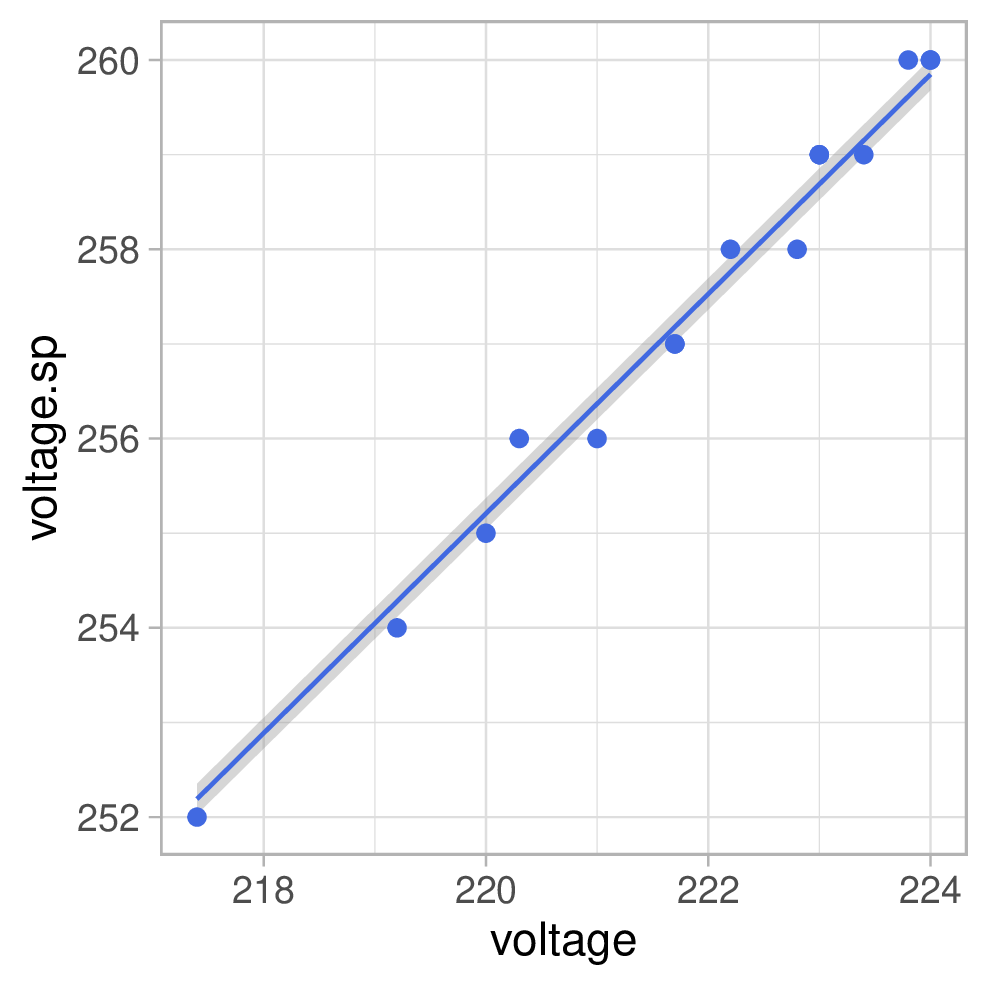
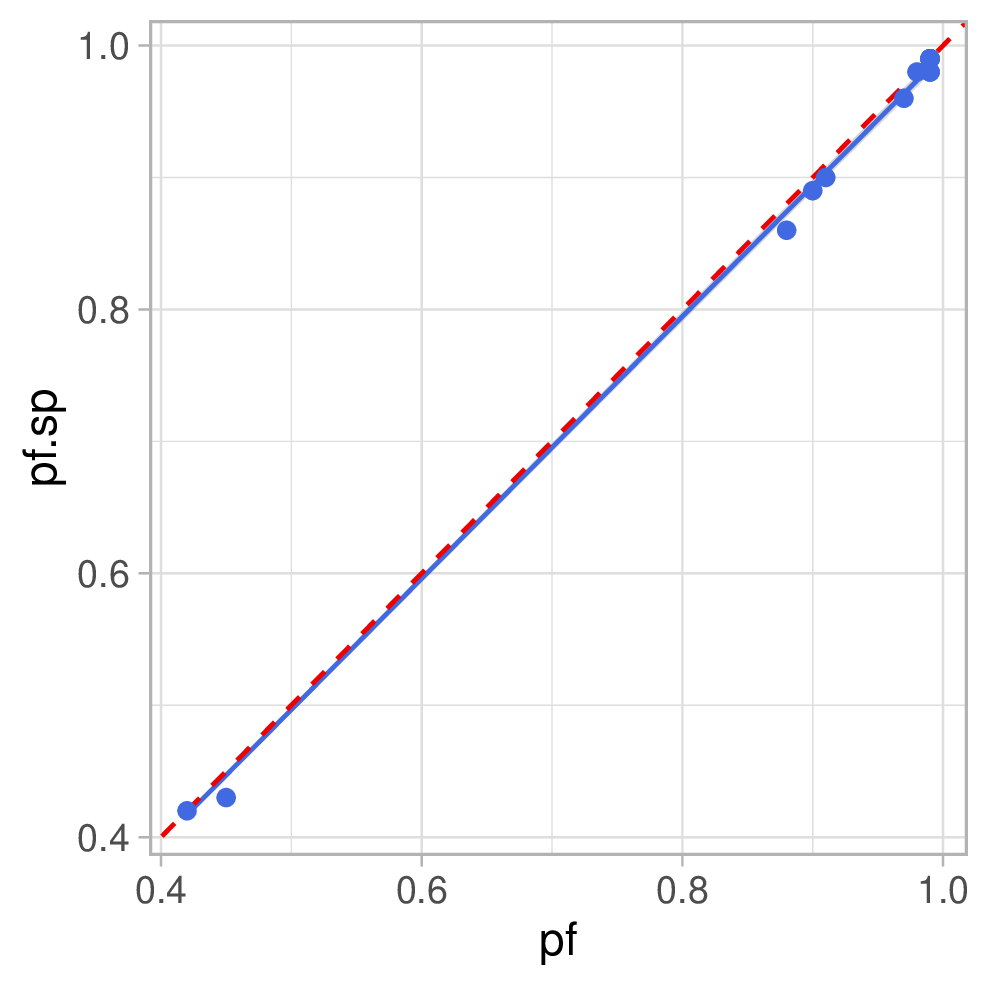
Und die dazugehörigen Geradengleichungen:
- \(P_{sp} = 1.025 \cdot P\)
- \(I_{sp} = 0.8955 \cdot I\)
- \(U_{sp} = 1.160 \cdot U\)
- \(λ_{sp} = 0.9933 \cdot \lambda\)
Für ganz pedantische habe ich zudem die beiden Modelle (mit und ohne Intercept) auch getestet (F-test) und der Unterschied war in keinem Fall signifikant (P = 0.7569, 0.1263, 0.1431, 0.1025).
Insgesammt gibt es also keinen Grund, den Intercept zu berücksichtigen.
Kalibriergleichung
Zur Kalibrierung brauchen wir aber die umgekehrte Richtung der obigen Gleichungen – d.h. wir haben \(P_{sp}\) gemessen und möchten wissen, was \(P\) ist. Also die Umkehrfunktion:
- \(P = 0.97561 \cdot P_{sp}\)
- \(I = 1.1167 \cdot I_{sp}\)
- \(U = 0.86207 \cdot U_{sp}\)
- \(λ = 1.0068 \cdot \lambda_{sp}\)
Ein kleines bisschen falsch ist das aber noch, weil wir ja auf dem Energie-Monitor auch immer den Verbrauch des Smartplugs mitmessen. Diese 0.3-0.8W, die eingangs erwähnt wurden. Analog beim Strom. D.h. streng genommen hätten wir vor der Berechnung der Kalibriergeraden diese Werte von den Referenzwerten abziehen müssen. Bei der Spannung spielt das keine Rolle und beim Leistungsfaktor bin ich mir nicht so sicher, aber der ist mir eh wurscht.
Spannung die Zweite
Vorhin hatte ich gesagt, dass man einen Variac bräuchte, um eine vernünftige Spannungsreihe zu generieren. Nun – ich habe zufällig einen...
Und so habe ich damit mal eine größere Spannbreite von Spannungswerten untersucht. Unter ≈100V steigt mein Energiemonitor aus und so habe ich diesmal das Multimeter als Referenz verwendet. Alle Werte wurden mit einer Last gemessen – dazu musste ein ungeregelter 80W Lötkolben herhalten.
Hier erstmal die Daten:
voltage voltage.sp
1 60.0 69
2 75.0 86
3 97.8 113
4 126.0 145
5 170.4 197
6 206.3 238
7 221.8 256
8 234.3 271
9 242.6 281
Und wie vorhin habe ich einen Plot gemacht und ein lineares Modell ohne Intercept gefittet:
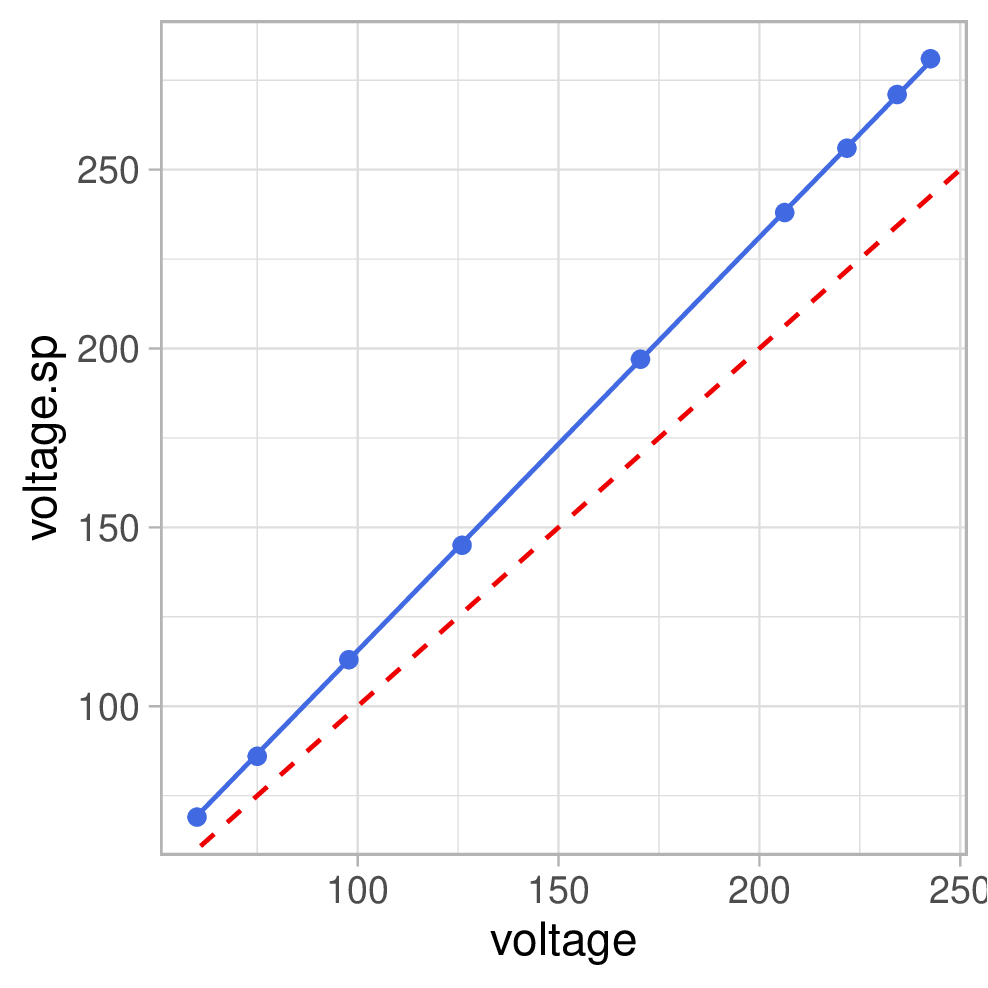
\(U_{sp} = 1.155 \cdot U\)
Lässt man einen Intercept zu beträgt dieser -0.7246V. Also vernachlässigbar.
Kalibrierung in der Praxis
Wie man anhand der Graphen und auch der Korrelationskoeffizienten sehen kann, ist unsere Kalibrierfunktion eine Gerade. D.h. wir haben nur zwei Parameter: Intercept und Steigung und wie wir gerade gesehen haben können wir den Intercept vernachlässigen und brauchen somit nur die Steigung.
In der Praxis bedeutet das, dass wir uns nicht jedes mal die Mühe machen müssen einen Haufen verschiedene Leistungen zu messen, um das Gerät zu kalibrieren. Eine einfache Einpunkt-Kalibrierung ist völlig ausreichend. D.h.:
- Last anschließen (Wasserkocher) und einschalten
- Refererenzwert am Energiemonitor ablesen (und ggf. 0.5W abziehen).
- Steigung ausrechnen (\(x/x_{sp}\)) oder von der jeweiligen Firmware ausrechnen lassen
Das macht man für Spannung, Strom und Leistung.
Nach erfolgter Kalibrierung zur Sicherheit eine Testmessung machen und schauen, ob alles passt.
Wer kein Energiemessgerät hat braucht eine Last mit bekannter Leistung. Die Spannung wird mit dem Multimeter gemessen und der Stom ergibt sich aus der Definition der elektrischen Leistung: \(I = P/U\).
Achung: das gilt nur, wenn der Leistungsfaktor mehr oder weniger bei 1 liegt! Deswegen nimmt man den Wasserkocher und keine Motoren oder elektronischen Geräte.
In eigener Software
Wenn man die Software in der die Messdaten verarbeitet werden sollen selbst geschrieben oder unter Kontrolle hat ist die Sache trivial. Einfach die Werte (v) anhand der obigen Kalibrierfunktion umrechnen:
v = a * v_sp
In TASMOTA
Das Vorgehen ist ausführlich in der original Doku von Tasmota beschrieben, aber ich gebe hier die essentiellen Schritte wieder.
In der verlinkten Anleitung steht "Adjust the power offset". Das ist falsch! Der Offset ist das was im linearen Modell Intercept (Deutsch: Achsenabschnitt) heißt – also ein Wert der auf den Messwert addiert wird. Was wir aber tatsächlich tun, ist die Steigung der Gerade anpassen. Die Durchführung ist aber völlig richtig erklärt.
Also:
- Last anschließen (Wasserkocher) und einschalten
- Refererenzwert am Energiemonitor ablesen (und ggf. 0.5W abziehen).
PowerSet xx.xin die Tasmota-Konsole eingeben. Dabei ist xx.x der korrekte (Referenz-) Wert.
Analog für Spannung (VoltageSet) und Strom (CurrentSet).
In ESPhome
Bei ESPhome muss der Kalibrierfaktor direkt in das YAML File des entsprechenden
Geräts. Im Netz finden sich verschiedene Anleitungen, die dazu einen
calibrate_linear Filter verwenden. Dabei übergibt man einen Haufen
Messwert-Paare für den jeweiligen Parameter – so wie wir es ganz oben selbst
gemacht hatten. Wie wir aber gelernt haben ist das nicht nötig. Eine
Einpunkt-Kalibrierung ist völlig ausreichend, solange sie sorgfältig gemacht
wird.
Was wir hier wirklich verwenden wollen ist der multiply Filter.
Bei anderen Sensoren mag es jedoch durchaus sinnvoll sein, calibrate_linear
zu verwenden, oder eine Kombination von multiply und offset.
Ein YAML Template für meinen Smartplug gibt es hier. Und die Kalibrierung macht man dann so (Beispiel für Spannung):
sensor:
[...]
- platform: hlw8012
[...]
voltage:
name: "${devicename} - Voltage"
unit_of_measurement: V
accuracy_decimals: 1
icon: mdi:flash-outline
filters:
- multiply: 0.8658
[...]
Man kann sich aber auch noch viel tiefgehender damit befassen – Fortsetzung folgt...