Ich liebe Spielzeug. Vor allem wenn es elektronisch ist. Eine ganz besondere Schwäche habe ich für Messgeräte aller Art. Und so besitze ich zahlreiche Geräte mit denen ich so ziemlich alles messen kann, was sich mir in den Weg stellt.

Natürlich sind darunter auch diverse Geräte zum Messen von Strecken oder Entfernungen: Zollstock, Bandmaß, Messschieber, Messschraube, Laser Entfernungsmesser und ein Laser-Rangefinder. Die beiden letzteren klingen auf den ersten Blick identisch und nutzen auch das gleiche Messprinzip, aber während die weit verbreiteten Laser-Entfernungsmesser für das Ausmessen im Haus gedacht sind, eignet sich der Rangefinder fürs Grobe – also größere Entfernungen bei mäßiger Genauigkeit. D.h. hier geht es nicht um Strecken im Bereich von ein paar Metern, die dann auf den Millimeter genau vermessen werden, sondern er zeigt seine Stärke beim Messen von Entfernungen in der Größenordnung von mehreren hundert Metern bei einer Genauigkeit von einem Meter oder so.

Das konkrete Modell, das ich besitze ist fernöstlicher Herkunft und heißt MILESEEY PF210 hunting, der für unter hundert Euro zu haben ist.

Das Datenblatt gibt folgende Merkmale an:

Parameter	Wert
Messbereich	3 – 800m
Genauigkeit	±0.5m + 0.01 digits
Vergrößerung	6x

Papier ist bekanntlich geduldig. Und da stellt sich die Frage, wie genau das Gerät tatsächlich misst. Aber was misst es überhaupt? Diverses:

• Entfernung in direkter Linie
• Steigungs-/Neigungswinkel über/unter der Horizontalen
• Horizontale Entfernung
• Höhe eines anvisierten Punkts über der horizontalen
• Höhendifferenz zwischen zwei Punkten
• Geschwindigkeit

Zudem hat es einen Regen/Nebelmodus, bei dem aus mehreren Messungen die am weitesten entfernte angezeigt wird.

Direkt messen kann das Gerät die Entfernung in direkter Line mittels Time of Flight Verfahren und den Neigungswinkel mittels eines elektronischen Sensors, wie man ihn auch in Smartphones oder den beliebten "Bevel Boxes" findet. Alles andere ist dann elementare Trigonometrie.

Im Folgenden konzentrieren wir uns aber auf die horizontale Entfernung, also die Entfernung in der Ebene.

Wie bestimmt man die Messqualität?

Die Qualität eines Messgeräts setzt sich aus zahlreichen Parametern zusammen. Z.B.:

1. Präzison (Reproduzierbarkeit der Messung)
2. Genauigkeit (Richtigkeit/accuracy)
3. Interferenzen (z.B. Tag/Nacht, Gegenlicht, Temperatur, Regen, ...)
4. Messbereich (Min/Max)
5. Linearität
6. Messzeit
7. ...

Die beiden ersten Aspekte wollen wir genauer untersuchen.

Präzision

Präzision ist die Wiederholgenauigkeit der Messung. D.h. wenn ich die gleiche Entfernung mehrfach messe – wie genau stimmen dann die erhaltenen Messwerte überein? Idealerweise sollten sie natürlich identisch sein, in der Praxis wird man aber meist leichte Abweichung von Messung zu Messung bekommen.

Dabei kann man ggf. noch eine ganze Reihe verschiedener Arten von Messwiederholungen betrachten:

• Unmittelbar hintereinander (within run precision)
• Mehrere Messserien – z.B. Nach dem wieder Einschalten (between run precision)
• An verschiedenen Tagen (between day precision)
• Verschiedene Bediener (between operator precision)
• Mehrere Geräte der Baureihe (between instrument precision)
• In verschiedenen Institutionen (between site precision)

Das volle Programm ist mir heute zu mühsam. D.h. unser Versuchsprotokoll sieht so aus:

• 10 verschiedene Distanzen (Gruppen)
• je 10 Messwiederholungen pro Gruppe
• Möglichst gute Abdeckung des Messbereichs von 3-800m

Insgesamt also 100 Messungen. Die dokumentieren wir in einer hübschen Tabelle und speichern diese im CSV Format und analysieren das Ganze. Alle Entfernungswerte sind in Metern.

Als erstes plotten wir mal die Wiederholungen der verschiedenen Gruppen. Die blaue Linie zeigt den Mittelwert der jeweiligen Gruppe:

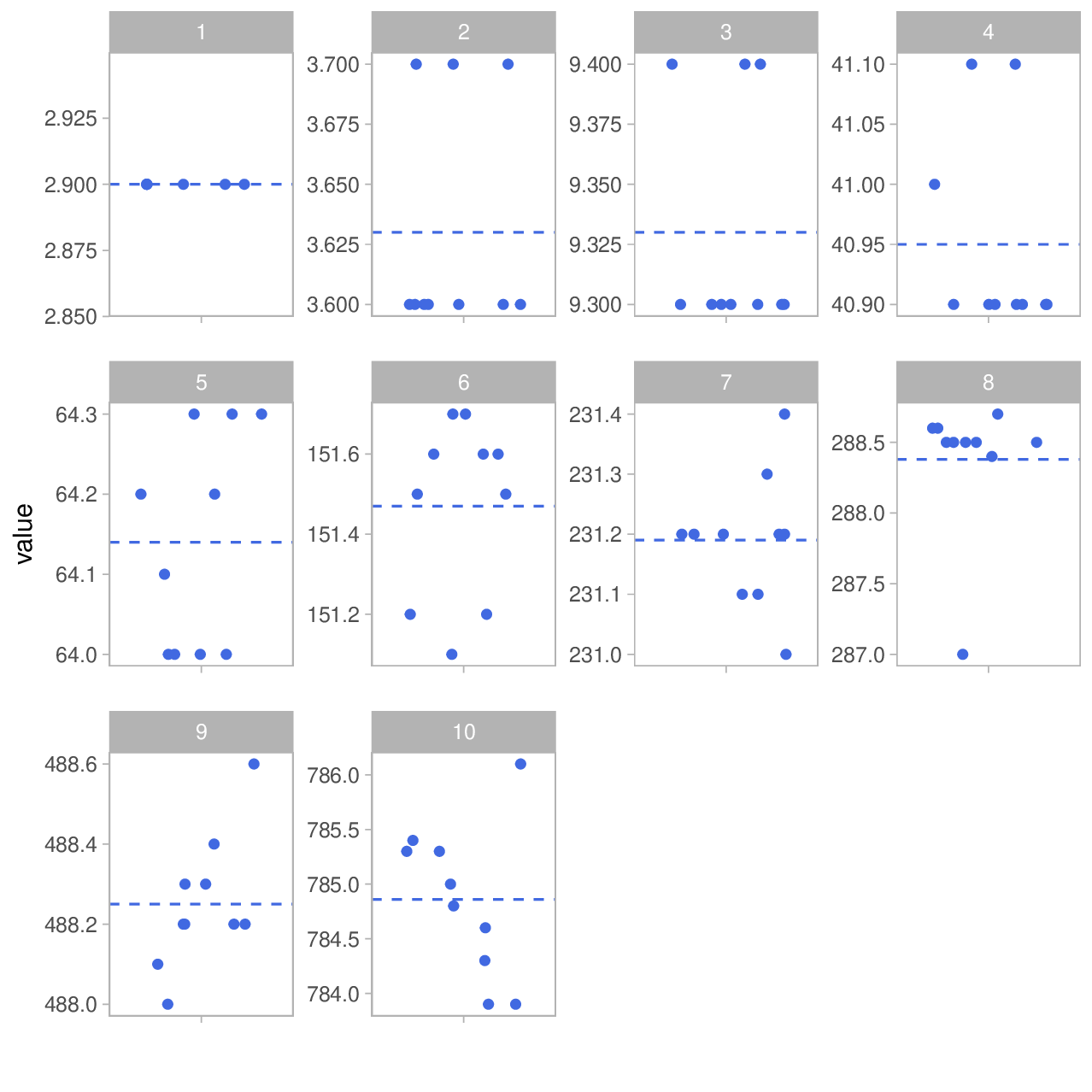
Wir decken also den Bereich von 2.9 bis ≈785m ab. Das ist schonmal top. Wer genau aufgepasst hat wird sich nun fragen, wie denn 2.9 m möglich waren, wo der Messbereich bei 3m anfängt. Des Rätsels Lösung ist, dass der direkte Abstand schon ≥3m ist, aber der horizontale Abstand nur 2.9m weil ich den Rangefinder leicht nach oben oder unten gehalten hatte. Und in der Tat fehlen hier auch einige Datenpunkte, weil der Messbereich unterschritten wurde.

Um besser beurteilen zu können, wie groß die Abweichung vom Gruppen-Mittelwert ist plotten wir das mal etwas anders.

D.h. die y-Achse zeigt die Abweichung vom Gruppen-Mittel. Letzteres ist im Titel der Mini-Plots gezeigt.

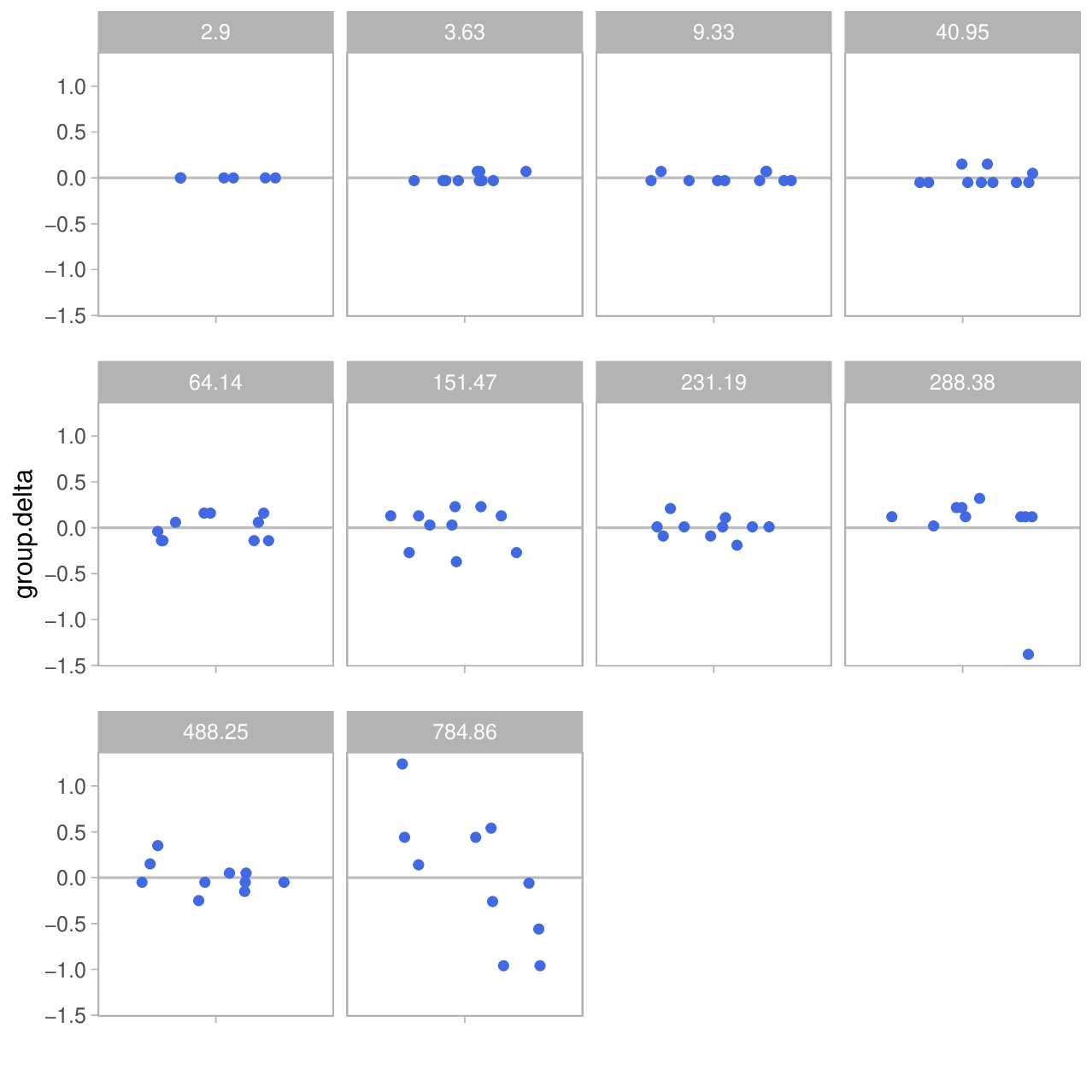
Wie man sieht ist die absolute Abweichung bei geringen Entfernungen sehr gering – kaum wahrnehmbar. Aber mit zunehmender Entfernung wächst sie bis zu ca. 1m bei knapp 800m. Man kann auch einigermaßen erkennen, dass bei niedrigen Distanzen die Abweichungen Vielfache von 0.1m sind – das ist die Genauigkeit mit der das Gerät seine Messwerte anzeigt. Nicht zu verwechseln mit der versprochenen Präzision...

Neben der absoluten Abweichung \(\Delta\) ist auch die relative Abweichung von Interesse. Hier in Prozent auf der y-Achse:

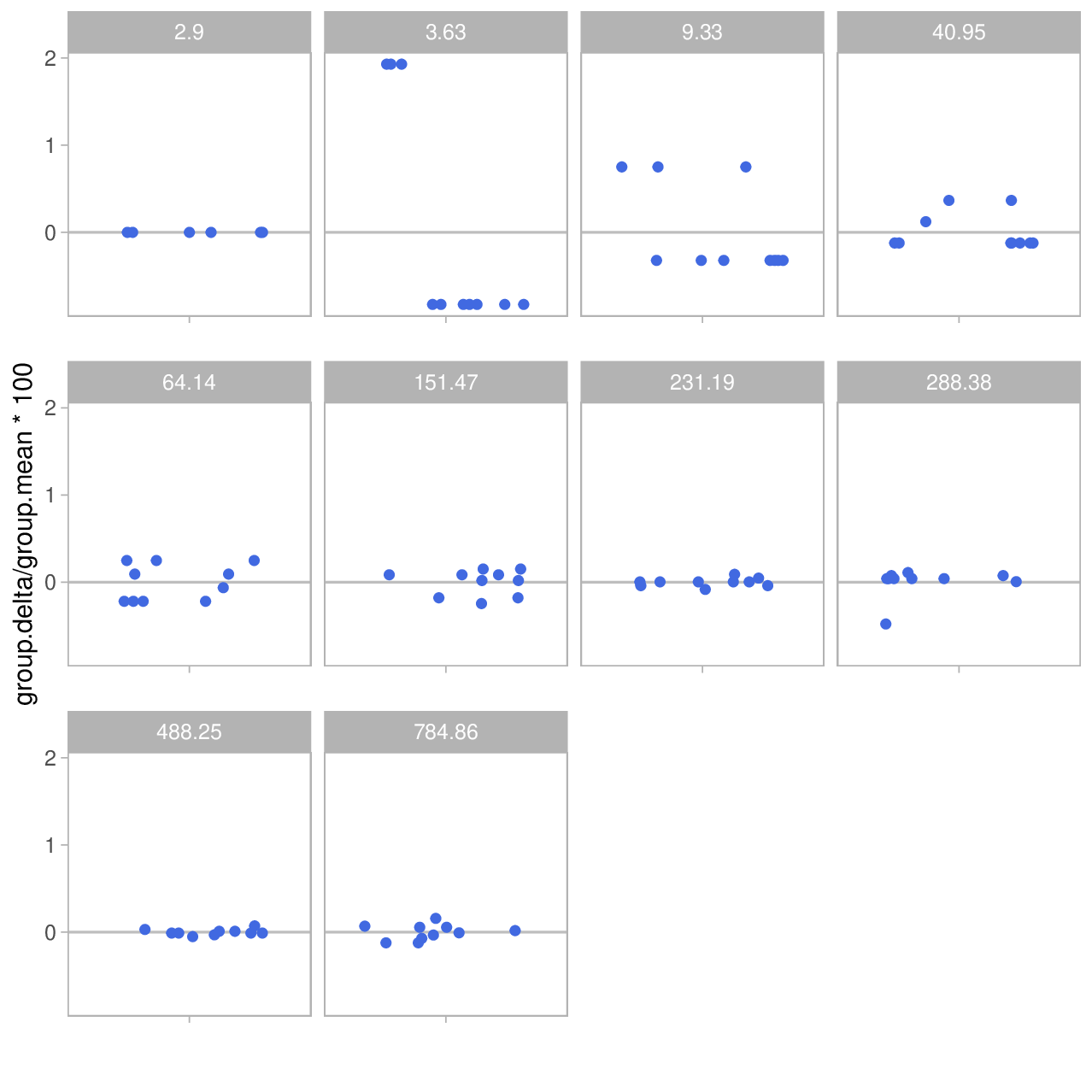
Und hier zeigt sich nun der umgekehrte Effekt im Vergleich zur absoluten Abweichung. Die relative Abweichung ist bei geringen Messwerten zunächst im Bereich von ± 1 bis 2% und fällt dann mit zunehmenden Entfernungen auf wenige Promille.

Um die Abweichungen in den Gruppen zu quantifizieren berechnen wir als nächstes die Standardabweichung (SD) innerhalb der Gruppen und zudem den Variationskoeffizienten (Coefficient of variation, CV). Letzterer errechnet sich als

Also die Standardabweichung normalisiert auf den Gruppen-Mittelwert. Das ist sinnvoll, weil bei vielen Messungen der Messfehler mit zunehmendem Messwert steigt. Hier die Plots, SD in Metern, CV in Prozent auf der y-Achse:

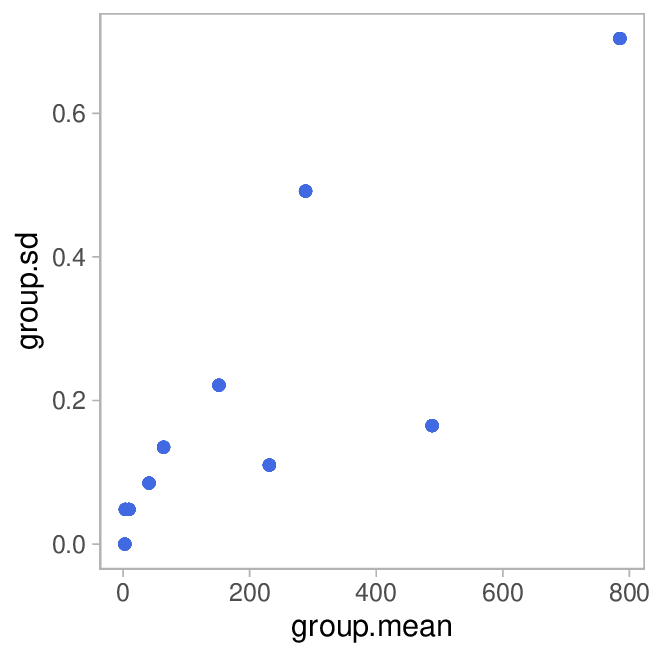
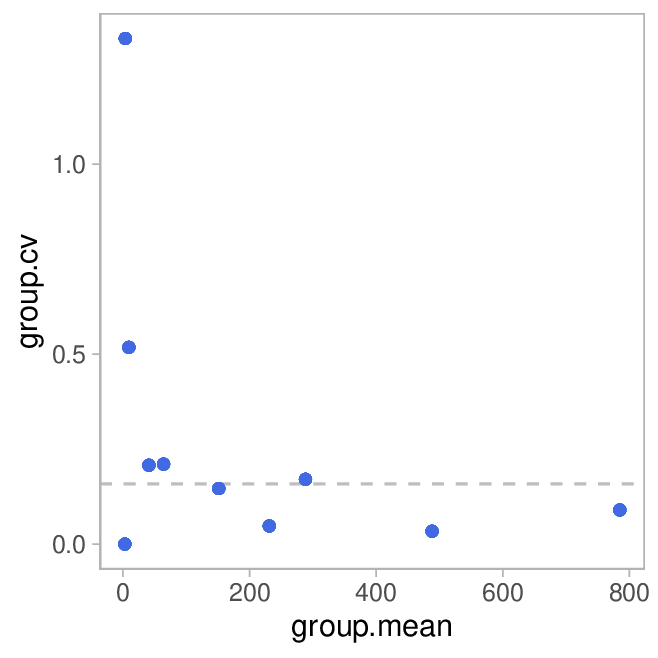
Die gestrichelte Linie repräsentiert den medianen Variationskoeffizienten.

Alles in Allem würde ich sagen, dass es in Sachen Präzision nichts zu meckern gibt.

Genauigkeit

Kommen wir zum zweiten Aspekt – der Korrektheit, AKA Genauigkeit, aka Trueness. Während es bei der Präzision darum ging, wie reproduzierbar die Messungen sind, wollen wir nun wissen, wie nah sie im Mittel an der Wahrheit liegen. Das ist eine Stufe anspruchsvoller, weil wir nun Referenzwerte brauchen, die die Wahrheit repräsentieren. Bei den Entfernungsbereichen, die wir hier abdecken ist das garnicht so simpel. Bei ein paar Metern könnte man ein Maßband bemühen, aber 500m? Meine Lösung lautet: Online-Karten. Sowohl bei Google Maps, als auch im Bayern-Atlas gibt es eine Messfunktion, bei der man die Entfernung zwischen manuell gesetzten Punkten auf der Karte ermitteln kann. Bis auf ein oder zwei Ausnahmen habe ich den Bayern-Atlas als Referenz verwendet.

Nun ist die so ermittelte Referenz-Entfernung aber auch nicht korrekt, sondern unterliegt Ungenauigkeiten oder Fehlern im Kartenmaterial und vor allem auch der Ungenauigkeit meiner manuellen Punktsetzung. D.h. das sollte man bei der Interpretation im Hinterkopf behalten.

Zudem ist auch die Entfernungsmessung mit dem Rangefinder nicht nur von der Qualität des Instruments ab, sondern auch von der Bedienung. Da steht man schnell einmal ein paar Handbreit weg vom optimalen Punkt oder visiert nicht exakt den in der Karte ausgewählten Punkt an.

Letztlich fließen beide Unsicherheiten in das Gesamtergebnis ein und machen dies schlechter, als es in einer idealen Welt wäre.

Mein Versuchsplan sieht 20 Einzelmessungen (\(value\)) und die dazugehörigen Referenzwerte (\(ref\)) vor. Schauen wir mal auf das Ergebnis. Zunächst als xy-Plot in dem wir die gemessen Entfernungen gegen die Referenzwerte plotten:

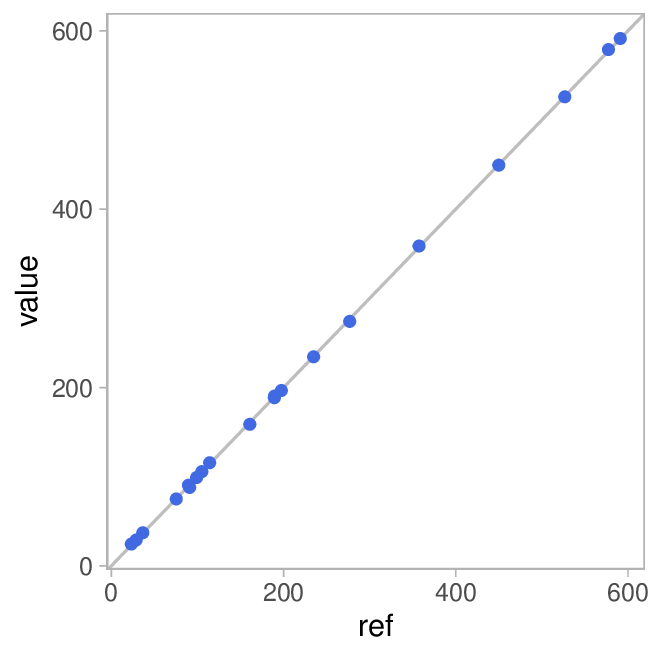
Die graue Diagonale stellt die Linie perfekter Übereinstimmung dar. Wie man sieht stimmen unsere Messungen sehr gut mit den Referenzwerten überein. Und auch der Korrelationskoeffizient stützt diese Einschätzung:

Und wenn wir ein lineares Modell fitten bekommen wir

Also hervorragend.

Um die Abweichungen besser beurteilen zu können machen wir aber zusätzlich noch einen sogenannten Bland-Altman Plot. Dabei wird auf der x-Achse der Mittelwert von Referenz und gemessenem Wert (\((value + ref)/2\)) aufgetragen und auf der y-Achse die Abweichung der Messung vom Referenzwert (\(value - ref\)). Auf diese Weise kann man sehr schön sehen, wie stark die Abweichungen in Abhängigkeit von der Distanz ist:

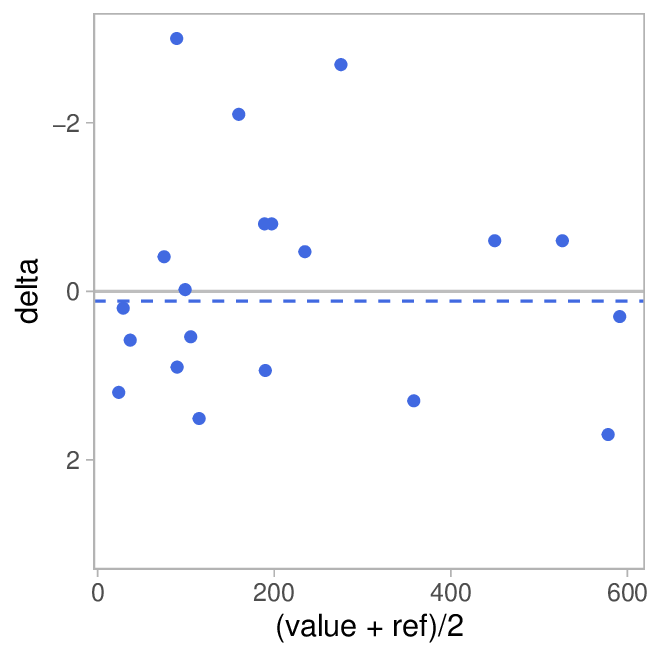
Die graue Line markiert perfekte Übereinstimmung (\(\Delta = 0\)) und die gestrichelte blaue die mittlere Abweichung (Bias).

Zuguterletzt erstellen wir noch eine Variante dieses Plot, bei dem wir statt der absoluten die relative Abweichung in Prozent auftragen:

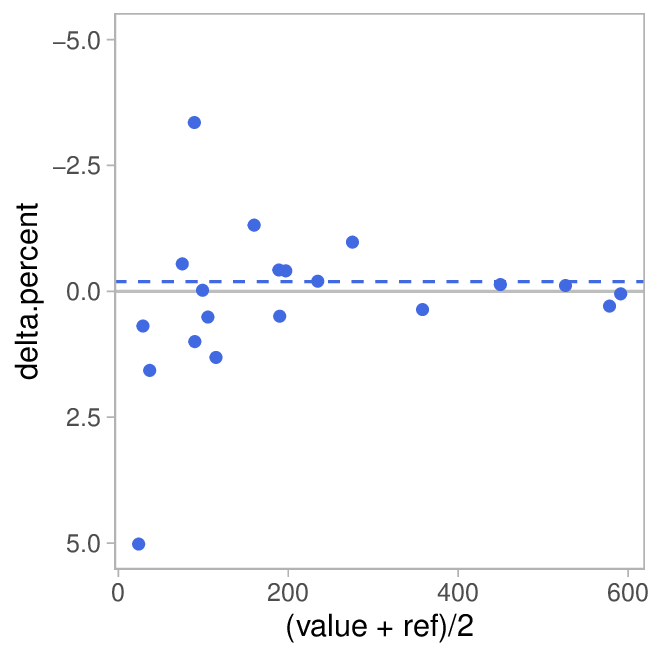
Der Vergleich der beiden Plots ist spannend: Während die absolute Abweichung über den Messbereich einigermaßen gleich bleibt resultiert das darin, dass die relative Abweichung bei geringen Distanzen noch recht hoch ist und dann stark abnimmt.

Fazit

Ich finde, mein preiswerter Rangefinder misst sehr reproduzierbar und richtig. Mehr Genauigkeit brauche ich definitiv nicht. Es wäre noch spannend, das gleiche auch für Geschwindigkeitsmessungen zu machen, aber da ist die Sache mit den Referenzwerten nochmal schwieriger. Vielleicht mache ich das irgendwann mal wenn ich Zeit habe.